UFRJ, Sem Campus, Cálculo 1, Listas de C1 - Profº Jair - Primeira Edição V1.3, Questão 4.4.15a
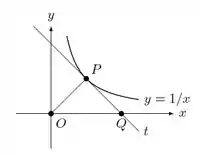
Na figura abaixo, é o ponto de tangência da reta com a curva . Sabendo que o ponto se desloca sobre a curva mostre que:
(a) O triângulo é sempre isósceles.
Passo 1
Fala, galera! Vamos resolver essa questão!
O enunciado pediu pra gente mostrar que o triângulo é sempre isósceles, ou seja, que ele tem sempre dois lados iguais.
Nós sabemos que o ponto é igual a e o ponto , na origem, é . Mas do ponto , nós só conhecemos a coordenadas (porque ele toca o eixo ), falta descobrir a coordenada desse ponto. Mas porque isso é importante?
Porque descobrindo o ponto , nós vamos conseguir verificar a distância de até e a distância de até . Se essas distâncias forem iguais, o triângulo terá dois lados iguais e será isósceles. Pra calcular a distância entre esses pontos, vamos usar a fórmula:
Vamos lá!
Passo 2
Pra encontrar a coordenada de , vamos usar a equação da reta tangente . A reta passa por e tem como coeficiente angular a derivada da função , que é . Então, no ponto dado, vamos ter:
Usando , temos:
Como o ponto é a interseção de com o eixo , fazendo , vamos ter:
Isolando :
Essa é a coordenada de .
Passo 3
Como , calculando a distância , vamos ter:
Agora vamos verificar a distância entre e :
Como as distâncias são iguais, nosso triângulo é isósceles, como queríamos demonstrar.
Valeu, galera! Até a próxima! 😉