UFRJ, Sem Campus, Cálculo 1, Listas de C1 - Profº Jair - Primeira Edição V1.3, Questão 4.4.15b
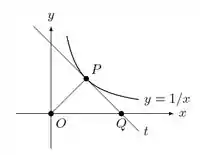
Na figura abaixo, é o ponto de tangência da reta com a curva . Sabendo que o ponto se desloca sobre a curva mostre que:
(b) A taxa de variaç��o da área do triângulo independe da velocidade com que o ponto se desloca.
Passo 1
Fala, galera! Vamos resolver essa questão!
O enunciado pediu pra gente mostrar que a variação da área do triângulo independente da velocidade com que o ponto se desloca.
Pra verificar isso, vamos definir a área do triângulo , que tá relacionada com sua altura e suas bases . Sendo assim, vamos verificar como varia a área, derivando a equação encontrada.
Vamos lá!
Passo 2
Como a área do triângulo é dada pelo produto da base pela altura divido por e o nosso triângulo tem altura e base , vamos ter a área:
Mas no ponto , . Então, substituindo em vai ficar:
Logo, a área do triângulo é sempre igual a . Se a gente derivar essa área, como a derivada de uma constante é nula, vamos ter:
Isso significa que não há variação de área, sua taxa é igual a zero, e por isso ela independe da velocidade com que o ponto se desloca.
Valeu, galera! Até a próxima! 😉