Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Taxa Relacionada

Ver Teoria
Exercício 174123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

USP, Sem Campus, Cálculo 1, Listas de Cálculo 1 - USP - Lista 1, Questão 5.11

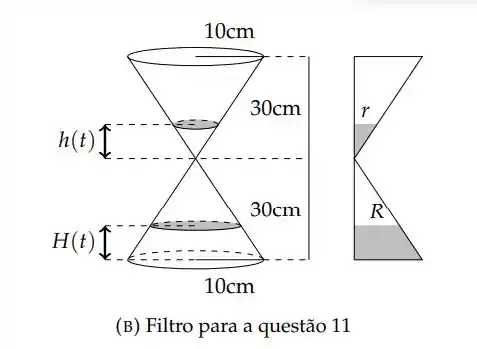
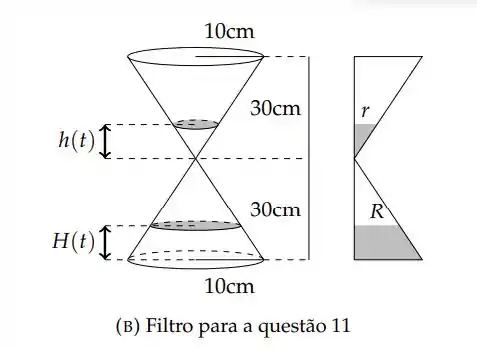
Num filtro com formato de cone, como na figura 3a, um líquido escoa da parte superior para a parte inferior passando por um orifício de dimensões desprezíveis. Num certo instante, a altura H do líquido depositado na parte inferior é 8 cm, a altura h do líquido da parte superior é 10 cm e h está diminuindo a uma taxa de variação instantânea de 2 cm/min. Calcule a taxa de variação de H em relação ao tempo nesse instante.

Passo 1

Eaew, belezinha?

Temos os seguintes dados da situação descrita no enunciado:

H ( t o ) = 8   c m , altura do líquido inferior no instante considerado;

h ( t o ) = 10   c m , altura do líquido superior no instante considerado;

r m = 10   c m , raio máximo dos cones;

A m = 30   c m , altura máxima dos cones;

d h d t = - 2   c m / m i n , taxa de variação instantânea de h ;

Como essas informações, temos que determinar a taxa de variação de H em relação ao tempo no instante considerado. Vamos lá!

Passo 2

Primeiro vamos olhar para a seção transversal do filtro:

Temos que o volume ocupado pelo líquido na parte superior é dado pelo volume do cone de raio r e altura h:

  V S = π   r 2 3 h

podemos relacionar o raio com altura do líquido por meio da regra de três

r h = 10 30

r = h 3

Então, substituindo no volume

  V S = π   ( h / 3 ) 2 3 h = π   h 3 27 .

Já o volume ocupado pelo líquido na parte inferior é dado pela diferença entre o volume do cone de raio r m e altura A m e o cone de raio R e altura ( A m - H ) :

  V I = π   r m 2 3 A m - π   R 2 3 ( A m - H )

podemos relacionar o raio com altura do líquido por meio da regra de três

R ( A m - H ) = 10 30

R = ( A m - H ) 3

Então, substituindo no volume

  V I = π   r m 2 3 A m - π   ( A m - H ) 3 3 = π   10 2 3 30 - π ( 30 - H ) 3   27 = 1000 π - π ( 30 - H ) 3   27 .

Passo 3

Temos que a variação temporal do volume inferior é igual ao negativo da variação temporal do volume superior, pois o líquido vai da parte superior para a inferior

d V I d t = - d V S d t

Substituindo

d d t ( 1000 π - π ( 30 - H ) 3   27 ) = - d d t ( π   h 3 27 )

derivando

d H d t ( 3 π ( 30 - H ) 2   27 ) = - d h d t ( 3 π   h 2 27 )

d H d t = - d h d t ( h 30 - H ) 2

Para o instante de interesse h = 10   c m , H = 8   c m e d h d t = - 2   c m / m i n , então

d H d t = - ( - 2 ) ( 10 30 - 8 ) 2 = 50 121 c m / m i n .

A questão foi isso! Te vejo na próxima! Tchau Tchau!

Resposta

d H d t = 50 121 c m / m i n .

Exercícios de Livros Relacionados

20. Caminhão na estrada O gráfico a seguir mostra a posição de um caminhão que percorre uma estrada. O caminhão parte em t = 0 e retorna 15 h mais tarde, em t = 15.a. Use a técnica descrita no Exemplo
(a) Encontre a taxa de variação média da área de um círculo em relação ao seu raio r quando r varia de i 2a3i i2a2,5i i i 2a2,1 (b) Encontre a taxa de variação instantânea quando r = 2 (c) Mostre que
O número de células de levedura em uma cultura de laboratório aumenta rapidamente no início, mas eventualmente estabiliza. A população é modelada pela função n = f t = a 1 + b e - 0,7 t Em que t é med
O rendimento total recebido da venda de x carteiras é R x = 200 x - 1 3 x 2 c) Ache o rendimento real da venda da trigésima primeira carteira.
A quantidade de carga Q , em coulombs (C), que passa através de um ponto em um fio até o instante t (medido em segundos) é dada por Q t = t 3 - 2 t 2 + 6 t + 2 Encontre a corrente quando (a) t = 0,5 s