UFCG, Sem Campus, Cálculo Diferencial e Integral I, Listas Cálculo 1 - UAMat - Lista 3 - Taxas Relacionadas, Questão 15
15 - Um homem começa a andar para o norte a a partir de um ponto . Cinco minutos depois uma mulher começa a andar para o sul a de um ponto ao leste de . A que taxa as pessoas estão se distanciando após a mulher começar a andar?
Passo 1
Fala aí, querido!! Tudo certinho? Bora resolver esse probleminha? 😉
Nesse problema temos um homem que está andando para o norte a partindo de um ponto . Cinco minutos depois uma mulher localizada a a leste de começa a andar para o sul a .
Com isso, queremos saber qual é a taxa de distanciamento depois que a mulher começou a andar.
Parece complicado, não é? 🤔
Passo 2
Primeiro vamos entender o movimento do sistema, pelas informações dada no problema, temos
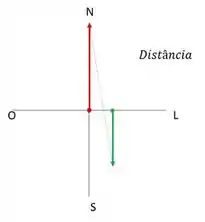
Onde a linha vermelha é o movimento do homem e a verde é o movimento da mulher.
Podemos dizer que o vetor deslocamento do homem é dado por
Dado que é a origem do sistema.
Já o vetor deslocamento da mulher é dado por
Dessa forma, podemos definir o vetor distanciamento entre eles como
Ou em seu modulo como
Tranquilo até aqui? 😉
Passo 3
Substituindo os vetores em , temos
Calculando o modulo desse vetor...
Derivando essa equação com relação a , podemos encontrar a taxa de variação da distância em relação ao tempo
Aplicando a regra da cadeia (a derivada de dentro multiplicada pela derivada de fora) ...
Voltando para e simplificando
Assim vamos descobrir que em depois que a mulher saiu, ou seja, , temos
Sacou como faz? Responde Aí! 😉
