Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Taxa Relacionada

Ver Teoria
Exercício 145123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

USP, Sem Campus, Cálculo 1, Listas de Cálculo 1 - USP - Lista 1, Questão 5.10

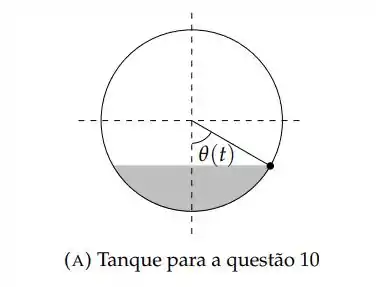
Uma mangueira está enchendo um tanque de gasolina que tem o formato de um cilindro “deitado” de diâmetro 2m e comprimento 3m. A figura 2a representa uma seção transversal do tanque no instante t. O ângulo θ varia de zero (tanque vazio) a π (tanque cheio). No instante em que a altura h do líquido é de 0.5m, a vazão é de 0.9m3/min. Determine a taxa de variação do ângulo θ nesse instante. Determine também a taxa de variação da altura h do neste mesmo instante.

Passo 1

Eaew, belezinha?

Temos os seguintes dados da situação descrita no enunciado:

d c = 2   m , diâmetro do cilindro;

C c = 3   m , comprimento do cilindro;

θ = 0 , tanque vazio;

θ = π , tanque cheio;

h , altura do líquido;

ϕ = 0,9   m 3 / m i n , vazão do líquido para h = 0,5   m ;

Como essas informações, temos que determinar d θ d t e d h d t no instante que h = 0,5   m . Vamos lá!

Passo 2

Primeiro vamos olhar para a seção transversal do cilindro:

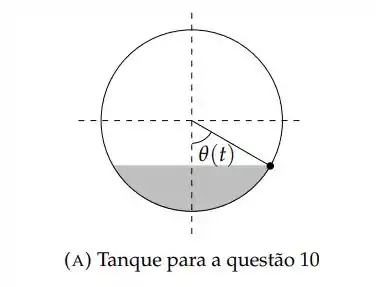
Temos que a área da seção varrida pela variação do ângulo θ é dada pela regra de três:

  π   r 2 2 π = A s θ

A S = π   r 2 2 π θ = ( 1 ) 2 2 θ = θ 2 .

Então, temos que a área da parte dessa seção que não tem líquido, o triângulo retângulo, é dada por

A T = c o s θ   s e n θ 2

Assim, temos que a área da área com líquido é dada por

A L = 2 ( A s - A T ) = θ - c o s θ   s e n θ

O volume então é:

V = C c A L = 6 ( A s - A T ) = 3 ( θ - c o s θ   s e n θ ) .

Passo 3

Temos que a vazão do líquido para h = 0,5   m é ϕ = 0,9   m 3 / m i n ,

ϕ = d V d t = 3 d d t ( θ - c o s θ   s e n θ ) = 3 d θ d t ( 1 - c o s θ 2 + s e n θ 2 ) = 3 d θ d t ( 2 - 2 c o s θ 2 )

Note que

r = 1 = c o s θ + h

h = 1 - c o s θ .

Substituindo

ϕ = 3 d θ d t ( 2 - 2 ( 1 - h ) 2 )

Para h = 0,5   m

ϕ = 0,9 = 3 d θ d t ( 2 - 2 ( 0,5 ) 2 )

d θ d t = 2 0,3 3 = 0,2   r a d / m i n .

Passo 4

Para encontrar a taxa de variação de h nesse instante, lembramos

h = 1 - c o s θ .

Derivando

d h d t = s e n θ d θ d t = 1 - c o s θ 2 1 d θ d t

Para h = 0,5   m , temos que c o s θ = 0,5 e d θ d t = 0,2   r a d / m i n ,

d h d t = 1 - 0 , 5 2 1 0,2 = 3 2 0,2 = 3 10 m / m i n .

A questão foi isso! Te vejo na próxima! Tchau Tchau!

Resposta

d θ d t = 0,2   r a d / m i n ;   d h d t = 3 10 m / m i n .

Exercícios de Livros Relacionados

20. Caminhão na estrada O gráfico a seguir mostra a posição de um caminhão que percorre uma estrada. O caminhão parte em t = 0 e retorna 15 h mais tarde, em t = 15.a. Use a técnica descrita no Exemplo
(a) Encontre a taxa de variação média da área de um círculo em relação ao seu raio r quando r varia de i 2a3i i2a2,5i i i 2a2,1 (b) Encontre a taxa de variação instantânea quando r = 2 (c) Mostre que
O número de células de levedura em uma cultura de laboratório aumenta rapidamente no início, mas eventualmente estabiliza. A população é modelada pela função n = f t = a 1 + b e - 0,7 t Em que t é med
O rendimento total recebido da venda de x carteiras é R x = 200 x - 1 3 x 2 c) Ache o rendimento real da venda da trigésima primeira carteira.
A quantidade de carga Q , em coulombs (C), que passa através de um ponto em um fio até o instante t (medido em segundos) é dada por Q t = t 3 - 2 t 2 + 6 t + 2 Encontre a corrente quando (a) t = 0,5 s