UFRJ, Sem Campus, Cálculo 1, Listas de C1 - Profº Jair - Primeira Edição V1.3, Questão 4.4.13
Uma mulher de de altura caminha em direção a um muro a uma razão de . Diretamente atrás dela e a do muro está um refletor acima do nível do solo.
Quão rápido o comprimento da sombra da mulher estará variando no muro quando ela estiver a meio caminho entre o refletor e o muro? A sombra está esticando-se ou encurtando-se?
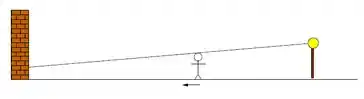
Passo 1
Fala, galera! Vamos resolver essa questão!
O enunciado pediu pra gente determinar a taxa com que a sombra da mulher estará variando no muro quando ela estiver a meio caminho entre o refletor e o muro.
Vamos chamar de a distância da mulher até o muro e o comprimento da sombra no muro. Então, nós queremos encontrar a variação . Pra isso, vamos observar a nossa figura e encontrar uma relação no triângulo, a qual podemos derivar, usar os dados do enunciado e encontrar a nossa variação.
Vamos lá!
Passo 2
Vamos começar considerando a reta saindo do refletor, passando pela cabeça da mulher até encontrar o muro. Assim, igualando do intervalo até e de até , obtemos que:
Fazendo meio pelos extremos, vamos ter:
Quando , temos o meio do caminho entre o refletor e o muro. Então, substituindo:
Isolando :
Passo 3
Derivando a nossa relação do triângulo, , vamos ter:
Então, substituindo , , (que é negativa porque diminuiu quando caminhamos na direção do muro), obtemos:
Isolando , temos a taxa com que a sombra da mulher estará variando no muro:
Portanto, a sombra está esticando-se.
Valeu, galera! Até a próxima! 😉