UFRJ, Sem Campus, Cálculo 1, Listas de C1 - Profº Jair - Primeira Edição V1.3, Questão 4.4.11
Um quadro de de altura é colocado em uma parede de tal forma que sua base esteja no mesmo nível dos olhos de um observador que está se aproximando da parede a uma velocidade de . Com que velocidade a medida do ângulo de visão do quadro estará variando quando o observador estiver a da parede?
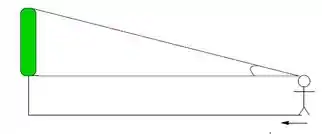
Passo 1
Fala, galera! Vamos resolver essa questão!
O enunciado pediu pra gente determinar a taxa com o ângulo de visão do quadro estará variando quando o observador estiver a da parede.
Vamos chamar de a distância entre a pessoa e a parede em função do tempo e de o ângulo de visão do quadro. Observando o triângulo retângulo da figura, podemos escrever a relação:
A gente quer obter , que é a variação do ângulo de visão. Pra isso, vamos derivar essa relação e usar os dados do enunciado.
Vamos lá!
Passo 2
Vamos começar derivando implicitamente a relação do passo anterior:
Sabendo que o quadro tem de altura e que a distância do observador é de , usando o teorema de Pitágoras, vamos achar o valor da hipotenusa:
Dessa forma, vamos ter . Sabendo que oobservador se aproxima da parede com uma velocidade (negativa porque a distância está diminuindo) e com o valor do cosseno, temos:
Resolvendo pra , vamos ter:
Que é a variação do nosso ângulo de observação.
Valeu, galera! Até a próxima! 😉