Um reservatório possui a forma de um cone circular reto com o vértice para baixo, tem de profundidade e de diâmetro. Esse reservatório é esvaziado à razão constante de .
Determine a razão segundo a qual o nível de água está descendo no instante em que a superfície da água está a do topo.
Passo 1
Fala, galera! Vamos resolver essa questão!
O enunciado pediu pra gente determinar a taxa de variação do nível da água, que nós vamos chamar de , em relação ao tempo. Pra isso, nós temos uma taxa de variação do volume , porque ele está sendo esvaziado, e um raio , que é metade do diâmetro.
Vamos esboçar o cone pra entender melhor:
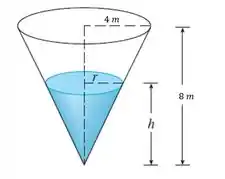
O que nós temos que fazer é encontrar quando . O volume e a altura são relacionados através da expressão do volume do cone:
Então, vamos tentar expressar em função apenas de , usando as relações de proporcionalidade da figura acima, derivar a expressão e substituir os dados para encontrar .
Vamos lá!
Passo 2
Olhando a figura do passo , nós conseguimos relacionar o raio e a altura através da equação:
Isolando , temos:
Substituindo esse valor de na expressão do volume , vamos ter:
Passo 3
Agora vamos derivar cada lado da equação acima em relação a :
Isolando :
Agora substituindo e , temos:
Isso significa que a água está descendo a uma taxa de .
Valeu, galera! Até a próxima! 😉