Um retângulo possui lados que variam com o tempo e está inscrito numa região triangular conforme a figura abaixo. Determine com que taxa a área do retângulo está variando no instante em que sua altura mede e está aumentando à taxa de . Nesse instante a área está aumentando ou diminuindo?
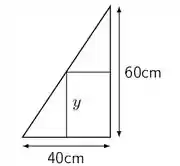
Passo 1
Fala, galera! Vamos resolver essa questão!
O enunciado nos deu um retângulo inscrito em um triângulo que está variando sua altura, e quer saber se a área do retângulo tá diminuindo ou aumentando, quando sua altura é e temos uma taxa de variação da altura .
Isso quer dizer que precisamos encontrar a taxa de variação da área . Como a área do retângulo é , definindo e como funções de , vamos obter derivando essa equação implicitamente. Só que pra isso a gente precisa descobrir o valor de , que vai ser a base do nosso retângulo. Nós conseguimos fazer isso definindo uma relação entre essas variáveis por semelhança de triângulos. Então, vamos lá!
Passo 2
Por semelhança de triângulos, olhando a figura, nós temos:
Com , vamos ter:
Passo 3
Agora vamos usar nossa relação novamente para derivar e encontrar .
Derivando implicitamente, temos:
Como , vamos obter:
Passo 4
Mas a gente quer saber como a varia a área do retângulo , então vamos derivar implicitamente essa equação, usando a regra do produto:
Usando os valores que encontramos, , , e , temos:
Então, a área tá diminuindo nesse instante.
Valeu, galera! Até a próxima! 😉