Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Taxa Relacionada

Ver Teoria
Exercício 109123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

UNICAMP, Sem Campus, Cálculo 1, Listas de Cálculo 1 - Profº Ricardo Martins - Lista sobre Derivadas, Questão 5.2

Um tanque de água possui o formato de um cone circular invertido, com base de raio 2 m e

altura igual a 4 m . Se a água está a sendo bombeada para o tanque a uma taxa de 2   m 3 / m i n ,

encontre a taxa na qual o nível da água está a aumentando quando a água estiver com 3 m

de profundidade.

Passo 1

Fala pessoal, tudo certinho com vocês? Vamos para mais uma questão de Cálculo. Dessa vez uma de taxa relacionada

Nosso objetivo é saber a taxa na qual o nível da água está a aumentando quando a água estiver com 3 m de profundidade

é informado que a água está sendo bombeada para o tanque a uma taxa de 2   m 3 / m i n

Passo 2

Vamos desenhar nosso cone

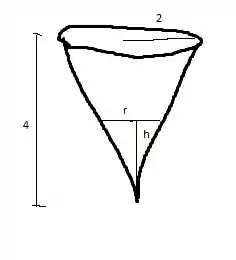
Vamos tentar escrever h em função de r . Usando semelhança de triângulos temos:

4 / h   a s s i m   c o m o   4 / r

⇒ h = r

Passo 3

Agora que sabemos que h   =   r . Vamos escrever a fórmula do volume do cone em função de h . Como o volume e a altura mudam, vamos colocar eles em função do tempo t . Logo

V ( t ) = π r ( t ) 2 h ( t ) / 3

V ( t ) = π h 3 ( t ) / 3

Agora que temos a relação entre volume e altura. Vamos derivar

V ' ( t ) = π h 2 ( t ) h ' ( t )

Passo 4

Agora que sabemos que

V ' ( t ) = π h 2 ( t ) h ' ( t )

e o enunciado diz que V ' ( t ) = 2   m 3 / m i n , basta substituirmos h ( t ) = 3 para descobrirmos a variação da altura quando a água está a 3 m de profundidade.

Então:

Se V ' ( t ) = 2   m 3 / m i n e h ( t ) = 3 . Logo

V ' ( t ) = π h 2 ( t ) h ' ( t )

⇒ 2 = π 9 h ' ( t )

⇒ h ' ( t ) = 2 9 π   m 3 / m i n

Prontinho pessoal!! Finalizamos mais uma questão. Espero que os passos tenham ficado claros. Até a próxima questão e bons estudos!!!! 😊

Resposta

Desenvolvimento acima

Exercícios de Livros Relacionados

20. Caminhão na estrada O gráfico a seguir mostra a posição de um caminhão que percorre uma estrada. O caminhão parte em t = 0 e retorna 15 h mais tarde, em t = 15.a. Use a técnica descrita no Exemplo
(a) Encontre a taxa de variação média da área de um círculo em relação ao seu raio r quando r varia de i 2a3i i2a2,5i i i 2a2,1 (b) Encontre a taxa de variação instantânea quando r = 2 (c) Mostre que
O número de células de levedura em uma cultura de laboratório aumenta rapidamente no início, mas eventualmente estabiliza. A população é modelada pela função n = f t = a 1 + b e - 0,7 t Em que t é med
O rendimento total recebido da venda de x carteiras é R x = 200 x - 1 3 x 2 c) Ache o rendimento real da venda da trigésima primeira carteira.
A quantidade de carga Q , em coulombs (C), que passa através de um ponto em um fio até o instante t (medido em segundos) é dada por Q t = t 3 - 2 t 2 + 6 t + 2 Encontre a corrente quando (a) t = 0,5 s