UFRJ, Sem Campus, Cálculo 1, Listas de C1 - Profº Jair - Primeira Edição V1.3, Questão 4.4.2
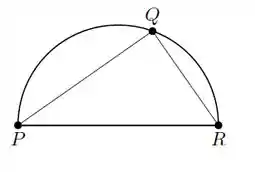
Um triângulo está inscrito num semicírculo de diâmetro conforme a figura abaixo. Sabendo que o vértice varia sobre o semicírculo e que o lado aumenta à razão de , determine a taxa com a qual a área do triângulo varia no instante em que o lado mede .
Passo 1
Fala, galera! Vamos resolver essa questão!
O enunciado pediu pra gente determinar a taxa com a qual a área do triângulo varia no instante em que o lado mede , sabendo que o lado tem (diâmetro do semicírculo onde ele tá inscrito) e que o lado aumenta à razão de (ou seja, ).
Repare que o triângulo é retângulo. Vamos chamar de o lado e de o lado . Assim, vamos poder usar o Teorema de Pitágoras para relacionar essas variáveis. Como queremos saber o quanto a área varia, vamos usar a fórmula de área do triângulo:
Mas a gente quer a variação, então precisamos derivar implicitamente essa equação. Quando fizermos isso, vai aparecer um termo , que vai ser determinado derivando implicitamente a relação obtida pelo teorema de Pitágoras, junto com os dados que o enunciado nos deu. Vai ficar mais claro a medida que formos resolvendo a questão.
Vamos lá!
Passo 2
Nós temos um triângulo retângulo com a hipotenusa . Então, com e , por Pitágoras, temos:
Quando , temos:
Passo 3
Agora podemos usar o teorema de Pitágoras novamente para encontrar . Então, derivando , temos:
Como a gente sabe que aumenta à razão de , temos . Além disso, temos e . Substituindo na equação, vamos ter:
Isolando :
Passo 4
Mas a gente quer saber como a varia a área do triângulo , então vamos derivar implicitamente essa equação, usando a regra do produto:
Mas nós encontramos , , e . Então, a variação da nossa área será:
Valeu, galera! Até a próxima! 😉