Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Teste da Razão e da Raiz

Ver Teoria
Exercício 581234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

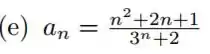
Passo 1

Bom, aqui não vale muito a pena fazer o teste da divergência, pois o limite vai dar zero. Vamos tentar simplificar esse termo aí. Perceba que:

n 2 + 2 n + 1 3 n + 2 < n 2 + 2 n + 1 3 n

Analisar esse cara depois do < é mais fácil (utilizamos o teste da comparação nesse passo). Podemos utilizar o teste da razão agora, que nada mais é que calcular:

lim n → ∞ ⁡ a n + 1 a n

Se esse limite estiver entre zero e um (incluindo o zero), a série converge. Se o limite for maior que um, a série diverge. Finalmente, se o limite for igual a um, não podemos concluir nada (temos que fazer outro teste)

Então, comecemos identificando os termos necessários:

a n = n 2 + 2 n + 1 3 n = n + 1 2 3 n

a n + 1 = n + 2 2 3 n + 1

Passo 2

Agora, vamos calcular o limite:

lim n → ∞ ⁡ n + 2 2 3 n + 1 n + 1 2 3 n = lim n → ∞ ⁡ n + 2 2 3 n + 1 3 n n + 1 2 = lim n → ∞ ⁡ 1 3 n + 2 n + 1 2 = lim n → ∞ ⁡ 1 3 1 + 2 / n 1 + 1 / n 2 = 1 3

Como o nosso limite está entre zero e um, temos que a série com termo geral n 2 + 2 n + 1 3 n converge. E como a nossa série é menor que ela, a nossa série também converge.

Resposta

A série converge.

Exercícios de Livros Relacionados

Determine se a série é absolutamente convergente, condicionalmente convergente ou divergente: ∑ n = 1 ∞ 1 + 1 n n 2
Determine se a série é absolutamente convergente ou condicionalmente convergente. ∑ n = 1 ∞ - 1 n - 1 n n 2 + 4
Determine se a série é absolutamente convergente, condicionalmente convergente ou divergente.9. ∑ n = 0 ∞ - 1 n 1,1 n n 4
Prove que, se ∑ a n for absolutamente convergente, então: ∑ n = 1 ∞ a n ≤ ∑ n = 1 ∞ a n
Demonstre o Teste da Raiz. [Sugestão para a parte (i): Tome qualquer número r tal que Lr1 e use o fato de que existe um inteiro N tal que a n nr quando n ≥ N .]