Diga se as séries são convergentes ou divergentes:
Passo 1
Oi, tudo bem? Essa série parece complicada, mas vou ajudar você aqui!
Para dizer se uma série diverge ou não, precisamos aplicar os testes! Mas qual escolher?
A cara da nossa série é
E podemos manipular um pouco aquele para termos uma série alternada:
E quando temos uma série alternada (esse é que nos diz isso) que envolve fatorial (aquele no denominador) a dica é aplicar o teste da razão para séries alternadas
Esse teste nos diz o seguinte:
Seja uma série do tipo
Fazendo o limite
Podemos ter três resultados diferentes:

Então a ideia aqui é o seguinte:
- identificar quem é na nossa série
- calcular
- determinar a razão
- calcular o limite dessa razão e comparar o resultado desse limite com as conclusões do teste =)
é isso! Mas relaxa, vou fazer passo a passo com você!
Passo 2
Nossa série é
E retirando a parte que alterna o sinal, , o aqui é o que sobra:
Beleza? Agora para calcular o é só trocar por nessa expressão:
Tranquilo até aqui?
Passo 3
Agora vamos calcular a razão :
Para simplificar o fatorial precisamos decompor o maior até chegar no menor :
E assim simplificar os fatoriais. Podemos simplificar também o termo em cima e embaixo:

Beleza?
Passo 4
Agora podemos passar para o limite!
Vamos calcular o limite dessa razão (e aqui vale todas as técnicas para cálculo de limites que você aprendeu lá no cálculo 1, ok?):
Quando , em cima o termo predominante é , por ter maior expoente. Já embaixo é o , único termo. Então no infinito temos o seguinte

Passo 5
Lembra das conclusões para o teste da razão para séries alternadas? Vamos relembrar:
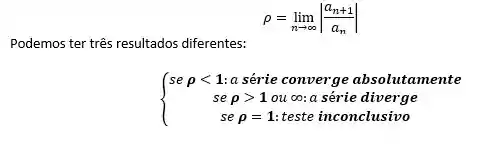
Como encontramos no passo anterior , esse valor se encaixa na primeira conclusão.
Portando, nossa série converge absolutamente.
Ufa! Terminamos!
Bora pra próxima?