Sabendo que é convergente, pode-se concluir a convergência de quais séries
Passo 1
Oi pessoal, tudo bem? Vamos começar?
O problema começa nos dando essa série aqui
E disse uma informação muito importante sobre ela: essa série converge
 Em seguida deu várias afirmativas, e perguntou quais delas são verdadeiras. Mas como assim concluir sobre a convergência de outras séries com base nessa aí?
Em seguida deu várias afirmativas, e perguntou quais delas são verdadeiras. Mas como assim concluir sobre a convergência de outras séries com base nessa aí?
 Isso mesmo, estamos falando em uma série convergente e, aplicando o teste da razão, podemos determinar o qual o raio de convergência! E assim tirar informações muito poderosas sobre outras séries! Tudo que estiver dentro do raio de convergência: converge! O que estiver fora, diverge! E o que estiver no limite, precisamos avaliar!
Isso mesmo, estamos falando em uma série convergente e, aplicando o teste da razão, podemos determinar o qual o raio de convergência! E assim tirar informações muito poderosas sobre outras séries! Tudo que estiver dentro do raio de convergência: converge! O que estiver fora, diverge! E o que estiver no limite, precisamos avaliar!
Então a ideia é achar o raio de convergência da série dada e depois avaliar item a item para ver o que conseguimos concluir!
Mas relaxa, vou fazer passo a passo com você!
Passo 2
A série dada foi essa aqui
Aplicando o teste da razão para convergência absoluta podemos encontrar o raio de convergência
Como essa série converge, sabemos que esse limite é . Tranquilo? Simplificando e comparando com um raio de convergência temos
Vemos que nesse caso! Então sabemos que se estiver nesse intervalo, a série é convergente!
 Beleza?
Beleza?
Agora vamos analisar alternativa por alternativa e ver se conseguimos alguma conclusão!
Passo 3
Olhando as três primeiras afirmativas temos o seguinte
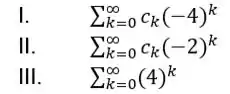
Note que a afirmativa está fora do nosso limite de convergência! Então não podemos dizer que ali em nossa série converge! O mesmo acontece com a segunda afirmativa!
Ela nos diz que , que está no limite do nosso intervalo! Como não sabemos a cara de , não podemos afirmar que converge! E a terceira afirmativa? Ela nem leva em consideração ! É uma série divergente pois
Logo é uma série divergente! Então eliminamos essas três primeiras!

Passo 4
Agora vamos analisar as duas últimas alternativas!
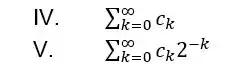
A alternativa pode ser escrita assim
E com isso temos que ! E esse valor está dentro do nosso raio de convergência e, portanto, essa série converge
E a ? Também! Olha o truque sujo aqui:
Temos que e está também dentro do raio de convergência, logo, essa série também é convergente!
Sendo assim, apenas as duas últimas alternativas estão corretas quanto a convergência, apenas as séries e convergem!
Beleza? Espero ter ajudado!
Até a próxima!