Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Teste da Razão e da Raiz

Ver Teoria
Exercício 591234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575860616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

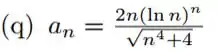
Passo 1

A primeira coisa que devemos fazer é realizar o teste da divergência. Calculando o limite.

lim n → ∞ ⁡ a n = lim n → ∞ ⁡ 2 n ln ⁡ n n n 4 + 4   = ∞ ∞

Nesse caso temos que usar a L’Hôpital e calcular as derivadas do numerador e do denominador.

Passo 2

Pra calcular a derivada do numerador vamos lembrar que e ln ⁡ a = a . Usando isso

ln ⁡ n n = e ln ⁡ ln ⁡ n n = e n ln ⁡ ln ⁡ n  

Usando a regra do produto.

d 2 n ln ⁡ n n d n = 2 e n ln ⁡ ln ⁡ n + 2 n d e n ln ⁡ ln ⁡ n d n

Aplicando a regra da cadeia.

d 2 n ln ⁡ n n d n = 2 ln ⁡ n n + 2 n e n ln ⁡ ln ⁡ n ln ⁡ ln ⁡ n + 1 ln ⁡ n

d 2 n ln ⁡ n n d n = 2 ln ⁡ n n - 1 ( n + n ( ln ⁡ n ) ln ⁡ ln ⁡ n + ln ⁡ n )  

Deu uma função bem feia, mas é isso mesmo. Vamos continuar

Passo 3

Calculando a derivada do denominador

d n 4 + 4 d n = 2 n 3 n 4 + 4

Logo o nosso limite será

lim n → ∞ ⁡ 2 ln ⁡ n n - 1 n + n ln ⁡ n ln ⁡ ln ⁡ n + ln ⁡ n 2 n 3 n 4 + 4 = lim n → ∞ ⁡ ln ⁡ n n - 1 n + n ln ⁡ n ln ⁡ ln ⁡ n + ln ⁡ n n 4 + 4 n 3

Tomando n 4 + 4 = n 2 1 + 4 / n 4 e abrindo esse limite em uma soma de limites

lim n → ∞ ⁡ n 2 1 + 4 n 4 n ln ⁡ n n - 1 1 + ln ⁡ n ln ⁡ ln ⁡ n n 3 + lim n → ∞ ⁡ n 2 1 + 4 n 4 ln ⁡ n n n 3

lim n → ∞ ⁡ 1 + 4 n 4 ln ⁡ n n - 1 1 + ln ⁡ n ln ⁡ ln ⁡ n + lim n → ∞ ⁡ 1 + 4 n 4 ln ⁡ n n n

O primeiro limite já tende a + ∞ então nem precisamos calcular o segundo para poder afirmar que

lim n → ∞ ⁡ a n ≠ 0

Logo a série diverge.

Resposta

A série diverge

Exercícios de Livros Relacionados

Determine se a série é absolutamente convergente, condicionalmente convergente ou divergente: ∑ n = 1 ∞ 1 + 1 n n 2
Determine se a série é absolutamente convergente ou condicionalmente convergente. ∑ n = 1 ∞ - 1 n - 1 n n 2 + 4
Determine se a série é absolutamente convergente, condicionalmente convergente ou divergente.9. ∑ n = 0 ∞ - 1 n 1,1 n n 4
Prove que, se ∑ a n for absolutamente convergente, então: ∑ n = 1 ∞ a n ≤ ∑ n = 1 ∞ a n
Demonstre o Teste da Raiz. [Sugestão para a parte (i): Tome qualquer número r tal que Lr1 e use o fato de que existe um inteiro N tal que a n nr quando n ≥ N .]