Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Caso Escalar

Ver Teoria
Exercício 331234567891011121314151617181920212223242526272829303132343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

11) Calcule a massa da superfície S parte do plano z = 2 - x dentro do cilindro x 2 + y 2 = 1 , sendo a densidade dada por ρ x ,   y ,   z = y 2 .

Passo 1

Bem, uma massa de um pedaço de superfície S é nos dado agora por uma integral de superfície caso escalar e sua cara é...

M S = ∬ S   ρ x ,   y ,   z   d S

Bem, como estamos trabalhando com uma integral de superfície, podemos muito bem utilizar o passo a passo maroto para detonar o problema imposto:

  1. 1º - Parametrizar a superfície S .
  2. 2º - Substituir os termos da parametrização na função ρ ( x ,   y ,   z ) .
  3. 3º - Encontrar o termo d S .

Passo 2

Vamos começar com o primeiro, onde no caso vamos parametrizar S . Por falar nisso, quem é a superfície? Para termos uma noção do que fazermos, recomendo fortemente que desenhe a superfície...

Um plano paralelo a x , z = 2 - x , e com restrição o cilindro de raio 1 ...

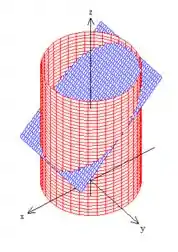
Bem, como a superfície é um pedaço de um plano, é válida uma parametrização explícita:

x = x

y = y

z = 2 - x

Não há mudança no x e no y , pois eles são os parâmetros. Então a parametrização é, de uma forma mais matematicamente elegante...

r → x ,   y = x ,   y ,   2 - x

Passo 3

Ok, agora nos falta a segunda parte do problema que é encontrar o domínio dos parâmetros: onde eles estão variando.

Bem, a superfície é um plano, mas ela está sendo delimitado dentro de um cilindro...

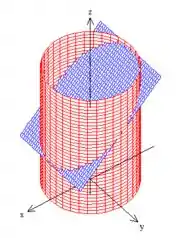
Se olharmos para a projeção dessa superfície no plano x y , o que vamos ver é exatamente esse disco D de raio igual ao do cilindro delimitador... r = 1 :

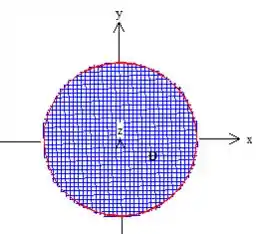
No momento, digamos apenas que x e y variam dentro de D .

Passo 4

Concluída esta etapa, encontremos a função ρ x ,   y ,   z que estamos integrando em termos dos parâmetros:

  ρ x ,   y ,   z = y 2

Como na parametrização x e y continuaram os mesmos e apenas z mudou, a função, continua mesma (pois nem depende de   z ):

  ρ r → x ,   y = y 2

Passo 5

Beleza, então podemos sair em busca do termo d S ...

d S = N →   d x d y

Onde esse vetor normal é dado por...

N → = ∂ r → x ,   y ∂ x × ∂ r → x ,   y ∂ y

Porém, como estamos trabalhando com uma parametrização em forma de um gráfico de função...

z = f x ,   y = 2 - x

Podemos utilizar o bizu de vetor normal para esse caso:

N → = - ∂ f ∂ x ,   - ∂ f ∂ y ,   1

N → = 1 ,   0 ,   1

Bem, ainda não concluímos o termo d S , pois ele nos exige o módulo de N → , então devemos extrair a raiz quadrada...

N → = 1 2 + 0 2 + 1 2

N → = 2

d S = 2     d x d y

Passo 6

Voltando para integral de linha que estamos resolvendo...

M S = ∬ S   ρ x ,   y ,   z   d S

E substituindo esses termos que determinamos (lembrando que S , trocamos por D que é a região de variação de x e y ).

∬ S   ρ x ,   y ,   z   d S = ∬ D   2     y 2 d x d y =

2   ∬ D     y 2 d x d y

Como D é um círculo de raio 1 :

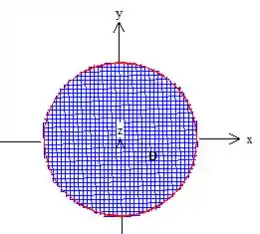
Calculemos com a mudança de coordenadas polares:

x = r cos ⁡ θ

y = r sin ⁡ θ

J = r

Onde r varia da origem até o raio limite do círculo - r = 1 …

0 ≤ r ≤ 1

E θ dá uma volta completa...

0 ≤ θ ≤ 2 π

2   ∬ D     y 2 d x d y = 2   ∫ 0 2 π ∫ 0 1 r sin ⁡ θ 2 ∙ J   d r d θ

2   ∫ 0 2 π ∫ 0 1 r 3 sin 2 ⁡ θ   d r d θ

Calculando a integral considerando sin 2 ⁡ θ constante perante r ...

2   ∫ 0 2 π sin 2 ⁡ θ ∫ 0 1 r 3   d r d θ =

2   ∫ 0 2 π sin 2 ⁡ θ r 4 4 0 1 d θ =

2 4   ∫ 0 2 π sin 2 ⁡ θ d θ =

Considerando agora que sin 2 ⁡ θ = 1 - cos ⁡ 2 θ 2 ...

2 4   ∫ 0 2 π sin 2 ⁡ θ d θ = 2 4   ∫ 0 2 π 1 2 - cos ⁡ 2 θ 2 d θ =

2 4   1 2 θ - sin ⁡ 2 θ 4 0 2 π =

2 4 π

Resposta

2 4 π

Exercícios de Livros Relacionados

Encontre a área da superfície com precisão de quatro casas decimais, expressando-a em termos de uma integral unidimensional e usando sua calculadora para estimar a integral.A Parte da superfície z = c
Calcule a integral de superfície. ∬ x 2 y z d S S é a parte do plano z = 1 + 2 x + 3 y que está acima do retângulo 0,3 × 0,2 .
Determine a área da superfície.A parte do cone z = x 2 + y 2 que se encontra entre o plano y = x e o cilindro y = x 2 .
Encontre a área da superfície com precisão de quatro casas decimais, expressando-a em termos de um a integral unidimensional e usando sua calculadora para estimar a integral.A Parte da superfície z =
Calcule a integral de superfície. ∬ x 2 + y 2 d S , S é a superfície com equação vetorial. r u , v =2 u v , u 2 - v 2, u 2 + v 2, u 2 + v 2 ≤ 1