Integral de superfície – Caso Escalar
Determine as equações paramétricas e a área da superfície obtida pela rotação da função , em torno do eixo .
(Não precisa resolver a integral)
Passo 1
Bom, vamos começar parametrizando essa superfície aí. Temos a função girando em torno do eixo .
Lembra que a gente tem um macete para parametrizar superfícies de revolução? Primeiro, vamos parametrizar a curva , pertencente ao plano . Como é uma curva, vamos usar como parâmetro, temos
Portanto, podemos parametrizar a curva assim
Como o problema diz que , temos .
Passo 2
Até ai beleza, né? Agora, para girar essa curva em torno do eixo , vamos imaginar que o “raio” de rotação é , a distância de cada ponto da superfície ao eixo . Para uma curva genérica que gira em torno do eixo , temos algo assim:
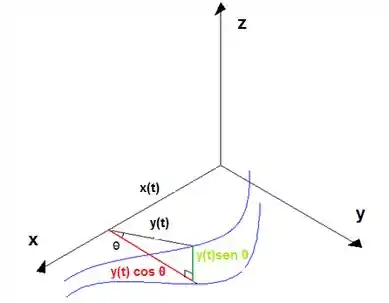
Girando um ângulo , podemos dizer que a variável da superfície se mantém a mesma da curva
E serve como raio de rotação. Fazendo as projeções da curva rotacionada, podemos ver que:
Em resumo: temos uma curva no plano e vamos girá-la em torno de . A variável , paralela ao eixo de rotação não se altera, . As outras duas variáveis serão escritas em função de , a coordenada da parametrização da curva que nos restou. Como é pertencente ao plano a curva, apresentará e , não pertencente, apresentará .
Beleza? Agora, como a parametrização da curva diz que
Podemos escrever, para a superfície
Ou seja, temos a parametrização
Como já tínhamos o intervalo da parametrização da curva, ele é o mesmo
Como temos uma volta completa em torno do eixo
Passo 3
Agora, vamos usar essa fórmula aqui para calcular a área da superfície:
Primeiramente, temo que calcular e
Passo 4
Calcular
Passo 5
Agora vamos montar a integral
Onde é o domínio da superfíce , que já encontramos
Substituindo na integral, temos:
Passo 6
Para simplificar a resposta, podemos integrar em relação a :
Pronto, como o problema não pede para calcularmos a integral, paramos por aqui.