Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Caso Escalar

Ver Teoria
Exercício 412356789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Determine a área da parte do paraboloide hiperbólico z = y 2 - x 2 que se encontra entre os cilindros x 2 + y 2 = 1 e x 2 + y 2 = 2 .

Passo 1

Vamos começar desenhando essa região. Temos um parabolóide (sela) cortado por dois cilindros centrados na origem, com raios 1 e 2 .:

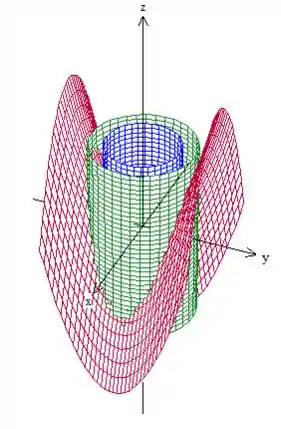
O problema nos pede então a área da parte do paraboloide que está entre os dois cilindros. Vendo de cima, temos isso aqui:

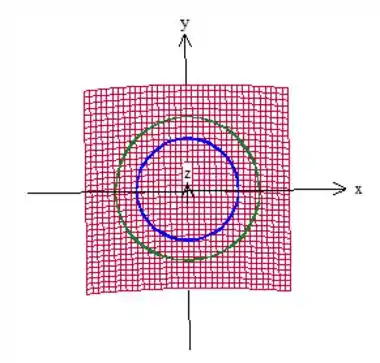
Beleza, vamos usar essa fórmula aqui para calcular a área da superfície:

A S = ∬ D   ∂ φ ∂ u × ∂ φ ∂ v d u d v

Passo 2

Agora precisamos parametrizar a superfície. Como nossa equação é z = y 2 - x 2 , vamos usar x e y como parâmetros, ok? Temos então:

φ x ,   y = ( x , y , y 2 - x 2 )

Onde x e y se encontram entre as circunferências verde e azul que desenhamos no passo anterior, a projeção da nossa superfíce cortada no plano x y .

Passo 3

Calcular ∂ φ ∂ x e ∂ φ ∂ y

∂ φ ∂ x = ( 1,0 , - 2 x )

∂ φ ∂ y = ( 0,1 , 2 y )

Passo 4

Calcular N → x ,   y

N → x , y = ∂ φ ∂ x × ∂ φ ∂ y

N → x , y = 1,0 , - 2 x × 0,1 , 2 y

N → x , y = i j k 1 0 - 2 x 0 1 2 y

N → x , y = ( 2 x , - 2 y , 1 )

N → x , y = 4 x 2 + 4 y 2 + 1

Passo 5

Agora vamos montar a integral

A S = ∬ D   4 x 2 + 4 y 2 + 1 d x d y

Onde D é a região entre as circunferências:

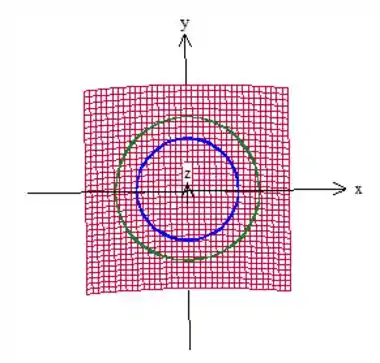
Que são os cilindros x 2 + y 2 = 1 e x 2 + y 2 = 2 vistos de cima. Bom, vamos usar coordenadas polares então, né?

x = r cos ⁡ θ

y = r   s e n   θ

J = r

Isso nos dá

A S = ∬ D *   4 r 2 cos 2 ⁡ θ + 4 r 2 s e n 2 θ + 1 r d r d θ

A S = ∬ D *   4 r 2 + 1 r d r d θ

Como a região completa uma volta no plano x y , temos 0 ≤ θ ≤ 2 π . O raio vai desde a circunferência azul até a verde, portanto, 1 ≤ r ≤ 2 . Susbstituindo na integral, temos:

= ∫ 0 2 π ∫ 1 2 4 r 2 + 1 r d r d θ =

Passo 6

Agora vamos resolver essa integral aí. Vamos fazer a substituição:

4 r 2 + 1 = u

8 r d r = d u         →           r d r = d u 8

r = 1         →         u = 5

r = 2         →         u = 9

= 1 8 ∫ o 2 π ∫ 5 9 u d u d θ =

= 1 12 ∫ o 2 π u 3 / 2 5 9 d θ =

= 1 12 ∫ o 2 π 27 - 5 5 d θ =

= 1 12 27 - 5 5 2 π =

= π 6 27 - 5 5

Resposta

π 6 27 - 5 5

Exercícios de Livros Relacionados

Encontre a área da superfície com precisão de quatro casas decimais, expressando-a em termos de uma integral unidimensional e usando sua calculadora para estimar a integral.A Parte da superfície z = c
Calcule a integral de superfície. ∬ x 2 y z d S S é a parte do plano z = 1 + 2 x + 3 y que está acima do retângulo 0,3 × 0,2 .
Determine a área da superfície.A parte do cone z = x 2 + y 2 que se encontra entre o plano y = x e o cilindro y = x 2 .
Encontre a área da superfície com precisão de quatro casas decimais, expressando-a em termos de um a integral unidimensional e usando sua calculadora para estimar a integral.A Parte da superfície z =
Calcule a integral de superfície. ∬ x 2 + y 2 d S , S é a superfície com equação vetorial. r u , v =2 u v , u 2 - v 2, u 2 + v 2, u 2 + v 2 ≤ 1