Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Caso Escalar

Ver Teoria
Exercício 491234567891011121314151617181920212223242526272829303132333435363738394041424344454647485051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Considere a parte ∑ do cilindro x 2 4 + y 2 = 1 que fica na intersecção das regiões x ≥ 0 , y ≥ 0 , e - y ≤ z ≤ y .

  1. Determine uma parametrização de ∑ , especificando o domínio de definição da parametrização.
  2. Calcule a integral de superfície ∬ ∑ 3 x   d S .

Passo 1

Primeiro note que a superfície está em cima de um cilindro com eixo no z como a gente está acostumado, porém, ele não é um cilindro com a base circular e sim, com uma base elíptica devido a sua equação x 2 4 + y 2 = 1 .

Desenhando esse cilindro no espaço, vamos obter:

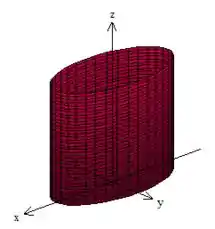
Porém, não queremos o cilindro todo, até porque ele é infinito :D, logo vamos pegar apenas a parte onde x ≥ 0 , y ≥ 0

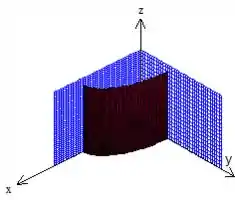
e delimitado por cima pelo plano z = y e por baixo pelo z = - y , dois planos passando paralelamente ao eixo x :

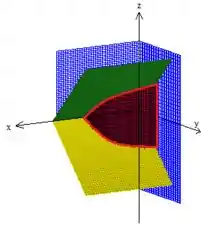
Prontinho! Superfície encontrada! É essa vermelhinha aí, percebeu?!: D

Passo 2

Item 1) como a superfície está em cima de um cilindro, nada mais justo que tentarmos uma parametrização cilíndrica!

Porém cuidado, o cilindro não tem uma base circular, mas sim elíptica, logo

x 2 = cos ⁡ θ         ⇒ o u     x = 2 cos ⁡ θ

y = sin ⁡ θ

z = z

Onde θ , como é um ângulo medido no plano X Y a partir do eixo x , teremos que ele deve dar um quarto de uma volta para preencher toda superfície, ou seja

0 ≤ θ ≤ π 2

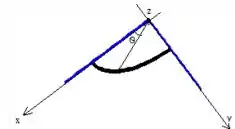
Quanto ao z , foi nos dado que ele varia de – y a y , logo, substituindo em coordenadas cilíndricas

- sin ⁡ θ ≤ z ≤ sin ⁡ θ

Logo, a parametrização pedida é

φ θ , z = ( 2 cos ⁡ θ , sin ⁡ θ ,   z )

Passo 3

Item 2) Como já possuímos a superfície ∑ parametrizada, a gente pode prosseguir procurando o nosso termo d S dado por

d S = ∂ φ ∂ θ × ∂ φ ∂ z d θ d z

Logo, devemos encontrar as derivadas parciais dessa superfície, e pra fazer isso, basta derivar parcialmente cada termo de φ ( θ ,   z ) , partiu?!:D

∂ φ ∂ θ = - 2 sin ⁡ θ , cos ⁡ θ ,   0

∂ φ ∂ z = 0 ,   0 ,   1

Lembrando de que

�� φ ∂ θ × ∂ φ ∂ z = i ^ j ^ k ^ - 2 sin ⁡ θ cos ⁡ θ 0 0 0 1

Resolvendo esse determinante

∂ φ ∂ θ × ∂ φ ∂ z = cos ⁡ θ ,   2 sin ⁡ θ , 0

Por fim, vamos calcular o módulo desse vetor, lembrando que módulo é a raiz das entradas ao quadrado

∂ φ ∂ θ × ∂ φ ∂ z = cos 2 ⁡ θ + 4 sin 2 ⁡ θ

Lembrando que cos 2 ⁡ θ pode ser substituído por 1 - sin 2 ⁡ θ , pela identidade trigonométrica fundamental, podemos simplificar essa raiz para

1 - sin 2 ⁡ θ + 4 sin 2 ⁡ θ = 3 sin 2 ⁡ θ + 1

Logo d S = 3 sin 2 ⁡ θ + 1   d z   d θ

Passo 4

Substituindo todos esses ingredientes na integral que queremos, inclusive a função nas novas coordenadas, vamos obter

∬ ∑ 3 x   d S = ∫ 0 π 2 ∫ - sin ⁡ θ sin ⁡ θ 3 ∙ 2 cos ⁡ θ 3 sin 2 ⁡ θ + 1 d z d θ

Agora é só resolver a integral iterada e correr para o abraço!:D

Então vamos lá, integrando primeiro em z e substituindo os limites de integração

∬ ∑ 3 x   d S = ∫ 0 π 2 3 ∙ 2 cos ⁡ θ 3 sin 2 ⁡ θ + 1 z 1 - sin ⁡ θ sin ⁡ θ d θ

∬ ∑ 3 x   d S = ∫ 0 π 2 6 cos ⁡ θ 3 sin 2 ⁡ θ + 1 sin ⁡ θ - - sin ⁡ θ d θ

∬ ∑ 3 x   d S = ∫ 0 π 2 2 ∙ 6 sin ⁡ θ cos ⁡ θ 3 sin 2 ⁡ θ + 1 d θ

Se a gente fazer uma substituição de 3 sin 2 ⁡ θ + 1 = u , d u = 6 sin ⁡ θ cos ⁡ θ d θ . Mas, não podemos nos esquecer dos limites de u , ou seja, quando θ = 0 → u = 3 sin 2 ⁡ 0 + 1 = 1 e θ = π 2 → u = 3 sin 2 ⁡ π 2 + 1 = 4 .

∬ ∑ 3 x   d S = 2 ∫ 1 4 u   d u = 2 ∙ 2 3 u 3 2 1 4

Substituindo os limites

∬ ∑ 3 x   d S = 2 16 3 - 2 3 = 28 3

Resposta

Item 1) φ θ , z = ( 2 cos ⁡ θ , sin ⁡ θ ,   z )

Onde

0 ≤ θ ≤ π 2

- sin ⁡ θ ≤ z ≤ sin ⁡ θ

Item 2)

∬ ∑ 3 x   d S = 28 3

Exercícios de Livros Relacionados

Encontre a área da superfície com precisão de quatro casas decimais, expressando-a em termos de uma integral unidimensional e usando sua calculadora para estimar a integral.A Parte da superfície z = c
Calcule a integral de superfície. ∬ x 2 y z d S S é a parte do plano z = 1 + 2 x + 3 y que está acima do retângulo 0,3 × 0,2 .
Determine a área da superfície.A parte do cone z = x 2 + y 2 que se encontra entre o plano y = x e o cilindro y = x 2 .
Encontre a área da superfície com precisão de quatro casas decimais, expressando-a em termos de um a integral unidimensional e usando sua calculadora para estimar a integral.A Parte da superfície z =
Calcule a integral de superfície. ∬ x 2 + y 2 d S , S é a superfície com equação vetorial. r u , v =2 u v , u 2 - v 2, u 2 + v 2, u 2 + v 2 ≤ 1