Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Caso Escalar

Ver Teoria
Exercício 581234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Questão 1: Seja a superfície parametrizada

r t ,   θ = 1 + t cos ⁡ θ ,   1 + t sin ⁡ θ ,   t 2 ,     t ,   θ ∈ 0 ,   2 × - π 4 , π 4

  1. Faça um esboço da imagem de r .
  2. Justifique se a imagem de r é uma superfície regular ou não.
  3. Calcule a equação implícita do plano tangente em 1 ,   0 .
  4. Calcule

∬ r   12 z x 2 + y 2 d S

Passo 1

L e t r a   A )

Bem, para fazer o esboço dessa superfície, é interessante levar para as coordenadas que sabemos reconhecer mais facilmente: as coordenadas cartesianas!

r t ,   θ = 1 + t cos ⁡ θ ,   1 + t sin ⁡ θ ,   t 2   →

x = 1 + t cos ⁡ θ

y = 1 + t sin ⁡ θ

z = t 2

Bem, se somarmos x 2 com y 2 , talvez simplificamos as contas, pois sin 2 ⁡ θ + cos 2 ⁡ θ = 1 ...

x 2 + y 2 = 1 + t 2 cos 2 ⁡ θ + 1 + t 2 sin 2 ⁡ θ →

x 2 + y 2 = 1 + t 2 cos 2 ⁡ θ + sin 2 ⁡ θ   →

x 2 + y 2 = 1 + t 2

Como

z = t 2   →       t = z   →

x 2 + y 2 = 1 + z 2

Ora, essa equação de x 2 + y 2 = 1 + t 2 no plano x y t é um paraboloide que passa por - 1 .

Agora, x 2 + y 2 = 1 + z 2 no espaço x y z , devido ao fato de z ≥ 0 , teremos apenas a parte de cima do paraboloide, até o z = 2 2 = 2 .

Além disso, a superfície que queremos tem o θ de...

θ ∈ - π 4 , π 4

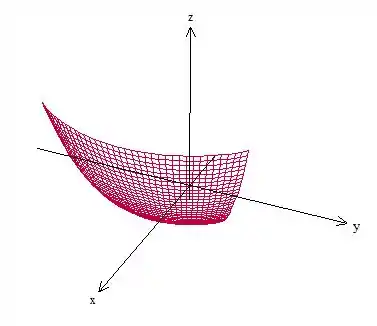
Viu só? Essa é a superfície S pedida

Passo 2

L e t r a   B )

Para isso, precisamos basicamente calcular o vetor normal a essa parametrização...

r t ,   θ = 1 + t cos ⁡ θ ,   1 + t sin ⁡ θ ,   t 2

Bem, pela nossa teoria, sabemos que o vetor normal é calculado desse jeito aqui:

N → = ∂ r ∂ t × ∂ r ∂ θ     →

∂ r ∂ t = cos ⁡ θ ,   sin ⁡ θ ,   2 t

∂ r ∂ θ = - 1 + t sin ⁡ θ ,   1 + t cos ⁡ θ ,   0

Logo, lembrando que produto vetorial é o calculo de um determinante...

N → = i → j → k → cos ⁡ θ sin ⁡ θ 2 t - 1 + t sin ⁡ θ 1 + t cos ⁡ θ 0   →

N → = - 2 t 1 + t sin ⁡ θ j → + 1 + t cos 2 ⁡ θ k → - 2 t 1 + t cos ⁡ θ i → - 1 + t sin 2 ⁡ θ k →   →

N → = - 2 t 1 + t sin ⁡ θ j → + 1 + t cos 2 ⁡ θ k → - 2 t 1 + t cos ⁡ θ i → + 1 + t sin 2 ⁡ θ k →   →

N → = - 2 t 1 + t cos ⁡ θ i → - 2 t 1 + t sin ⁡ θ j → + 1 + t k →   →

N → = - 2 t 1 + t cos ⁡ θ ,   - 2 t 1 + t sin ⁡ θ ,   1 + t

Prontinho! Agora basta verificar se esse vetor normal se anula em algum ponto do intervalo de interesse:

t ,   θ ∈ 0 ,   2 × - π 4 , π 4

Como 1 + t é sempre diferente de 0 nesse intervalo, o nosso vetor normal nunca é 0 ! Logo, se trata de uma superfície regular

Passo 3

L e t r a   C )

A equação implícita do plano tangente tem essa cara aqui:

N → t 0 ,   θ 0 ⋅ x ,   y ,   z = D   →

Onde N t 0 ,   θ 0 = N 1 ,   0 …

N → 1 ,   0 = - 2 1 + 1 cos ⁡ 0 ,   - 2 1 + 1 sin ⁡ 0 ,   1 + 1   →

N → 1 ,   0 = - 4 ,   0 ,   2

Então...

N → t 0 ,   θ 0 ⋅ x ,   y ,   z = D   →

- 4 ,   0 ,   2 ⋅ x ,   y ,   z = D

Basicamente agora falta saber quem é o D . Ora, sabemos que o ponto é tangente da nossa superfície:

r t ,   θ = 1 + t cos ⁡ θ ,   1 + t sin ⁡ θ ,   t 2 →

r 1 ,   0 = 1 + 1 cos ⁡ 0 ,   1 + 1 sin ⁡ 0 ,   1 2 →

r 1 ,   0 = 2 ,   0 ,   1

Esse ponto, pertence ao plano, então...

- 4 ,   0 ,   2 ⋅ 2 ,   0 ,   1 = D   →

- 8 + 0 + 2 = D   →

D = - 6

Logo, a equação do plano é...

- 4 ,   0 ,   2 ⋅ x ,   y ,   z = - 6   →

- 4 x + 2 z = - 6

Passo 4

L e t r a   D )

Ok, agora vamos calcular essa integral de superfície:

∬ r   12 z x 2 + y 2 d S

Para isso, primeiro devemos levar essa função que estamos integrando para os termos da parametrização, ok?

12 z x 2 + y 2   →

Como

x 2 + y 2 = 1 + t 2

z = t 2

Então...

12 z x 2 + y 2 = 12 t 2 1 + t 2 =

12 t 1 + t 2 = 12 t 1 + t

Passo 5

Então lembrando-se agora que...

d S = N →   d t d θ   →

N → = - 2 t 1 + t cos ⁡ θ 2 + - 2 t 1 + t sin ⁡ θ 2 + 1 + t 2   →

N → = 4 t 2 1 + t 2 cos 2 ⁡ θ + 4 t 2 1 + t 2 sin 2 ⁡ θ + 1 + t 2   →

N → = 4 t 2 1 + t 2 + 1 + t 2   →

N → = 1 + t 2 4 t 2 + 1   →

N → = 1 + t 4 t 2 + 1

Passo 6

Agora finalmente jogando tudo na integral...

∬ r   12 z x 2 + y 2 d S = ∫ - π 4 π 4 ∫ 0 2 12 t 1 + t   1 + t 4 t 2 + 1 d t d θ =

∫ - π 4 π 4 ∫ 0 2 12 t 4 t 2 + 1 d t d θ

Podemos calcular tal integral fazendo uma pequena mudança...

4 t 2 + 1 = x   →

d x = 8 t   d t     o u         t d t = d x 8

Mudando também os limites de integração...

t = 0     →         x = 1

t = 2     →         x = 9

∫ - π 4 π 4 ∫ 0 2 12 t 4 t 2 + 1 d t d θ = ∫ - π 4 π 4 ∫ 1 9 12 x d x 8 d θ =

3 2 ∫ - π 4 π 4 ∫ 1 9 x 1 2 d x d θ = 3 2 ∫ - π 4 π 4 2 3 x 3 2 1 9 d θ =

3 2 ∫ - π 4 π 4 2 3 x x 1 9 d θ =

Substituindo os limites de integração...

3 2 ∫ - π 4 π 4 2 3 - 2 3 9 9 d θ = 3 2 ∫ - π 4 π 4 2 3 - 18 d θ =

- 52 3 ⋅ 3 2 π 4 - - π 4 =

- 26 π 2 = - 13 π

Resposta

Letra A)

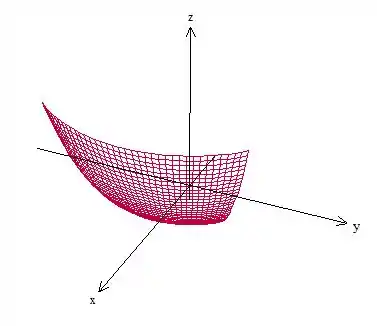
Letra B) É regular!

Letra C) - 4 x + 2 z = - 6

Letra D) - 13 π

Exercícios de Livros Relacionados

Encontre a área da superfície com precisão de quatro casas decimais, expressando-a em termos de uma integral unidimensional e usando sua calculadora para estimar a integral.A Parte da superfície z = c
Calcule a integral de superfície. ∬ x 2 y z d S S é a parte do plano z = 1 + 2 x + 3 y que está acima do retângulo 0,3 × 0,2 .
Determine a área da superfície.A parte do cone z = x 2 + y 2 que se encontra entre o plano y = x e o cilindro y = x 2 .
Encontre a área da superfície com precisão de quatro casas decimais, expressando-a em termos de um a integral unidimensional e usando sua calculadora para estimar a integral.A Parte da superfície z =
Calcule a integral de superfície. ∬ x 2 + y 2 d S , S é a superfície com equação vetorial. r u , v =2 u v , u 2 - v 2, u 2 + v 2, u 2 + v 2 ≤ 1