Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Caso Escalar

Ver Teoria
Exercício 971234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071727374757677787980818283848586878889909192939495969899100

Enunciado

9) Calcule ∬ S f ( x , y , z ) d S , onde

d) f x , y , z = z e S é a superfície do sólido limitado pelo cilindro x 2 + y 2 = 1 e os planos z = 1 e x + z = 4 .

Passo 1

Vamos lá, essa questão aqui vai ter uma grande diferença das outras que estamos fazendo, a gente acaba nem reparando se ler muito rápido. É o seguinte, as superfícies estávamos vendo quase sempre eram limitadas por outras, certo? Então, por exemplo, a parametrização de uma esfera cortada por um plano é simplesmente uma parte da esfera.

Essa questão aqui não é assim! Perceba que ele diz que S é a superfície do sólido, por isso S engloba todas as três superfícies que o compõe, ou seja, o cilindro x 2 + y 2 = 1 e as duas “tampas”, embaixo z = 1 e em cima x + z = 4 . Um esboço rápido é esse aqui:

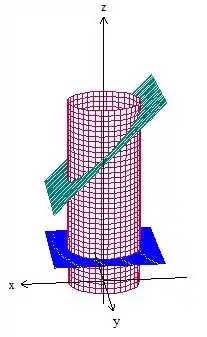
Vamos ter que encontrar uma parametrização, os limites de integração e o vetor normal para cada uma dessas três superfícies, vamos organizar tudo antes então!

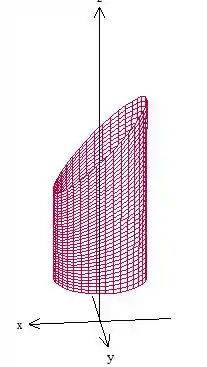
A superfície I vai ser o cilindro:

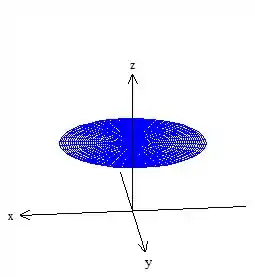
A superfície I I vai ser a tampa de baixo

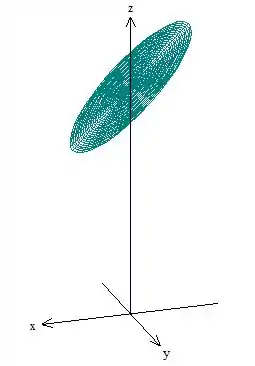
E a superfície I I I vai ser a tampa de cima

Passo 2

Vamos começar pela superfície I , sua parametrização cilíndrica é essa aqui:

x = cos ⁡ θ

y = sen ⁡ θ

z = z

Seu limite em θ é o de uma volta completa

0 ≤ θ ≤ 2 π

Por sua vez, z varia entre os dois planos z = 1 e z = 4 - x

1 ≤ z ≤ 4 - cos ⁡ θ

A normal dessa superfície vai ser encontrada pela fórmula

N → = ∂ φ ∂ θ × ∂ φ ∂ z

As derivadas vão ser essas aqui

∂ φ ∂ θ = - sen ⁡ θ , cos ⁡ θ , 0

∂ φ ∂ z = ( 0,0 , 1 )

N → = i j k - sen ⁡ θ cos ⁡ θ 0 0 0 1

= cos ⁡ θ , sen ⁡ θ , 0

N → = cos 2 ⁡ θ + sen 2 ⁡ θ = 1 = 1

Passo 3

Jogando tudo na integral

∬ S I z d S = ∫ 0 2 π ∫ 1 4 - cos ⁡ θ z d z d θ

= ∫ 0 2 π z 2 2 z = 1 z = 4 - cos ⁡ θ d θ = 1 2 ∫ 0 2 π 4 - cos ⁡ θ 2 - 1 d θ

= 1 2 ∫ 0 2 π 16 - 8 cos ⁡ θ + cos 2 ⁡ θ - 1 d θ

Aqui vamos ter que substituir cos 2 ⁡ θ = 1 + cos ⁡ 2 θ 2 , fica assim:

1 2 ∫ 0 2 π 31 2 - 8 cos ⁡ θ + cos ⁡ 2 θ 2 d θ =

= 1 2 31 θ 2 - 8 sen ⁡ θ + sen ⁡ 2 θ 4 θ = 0 θ = 2 π

Aqui todos os senos vão zerar! Sobrando só a primeira fração:

= 1 2 31.2 π 2 = 31 π 2

Passo 4

Vamos para a nossa primeira tampa, a superfície I I presente no plano z = 1 . Ela é um círculo, certo? Se fosse no plano x y já iriamos parametrizar sem nem precisar pensar muito como

x = r cos ⁡ t

y = r sen ⁡ t

Aqui vai ser a mesma coisa, além disso,

z = 1

Pronto, agora faltam os limites! A superfície é limitada pelo cilindro x 2 + y 2 = 1 , portanto

0 ≤ r ≤ 1

0 ≤ θ ≤ 2 π

A normal é essa aqui

∂ φ ∂ r = cos ⁡ t , sen ⁡ t ,   0

∂ φ ∂ t = - r sen ⁡ t ,   r cos ⁡ t ,   0

N → = i j k cos ⁡ t sen ⁡ t 0 - r sen ⁡ t r cos ⁡ t 0

= 0,0 , r cos 2 ⁡ t + r   sen 2 ⁡ t = 0,0 , r

N → = r 2 = r

Passo 5

Jogando tudo isso na integral

∬ S I I z d S = ∫ 0 2 π ∫ 0 1 1 . r d r d θ

= ∫ 0 2 π r 2 2 r = 0 r = 1 d θ = 1 2 ∫ 0 2 π d θ =

= 1 2 2 π = π

Passo 6

Vamos para a nossa última superfície, a sua parametrização vai ser muito parecida com a outra tampa. A superfície I I I é o plano z = 4 - x limitado pelo cilindro x 2 + y 2 = 1 , certo? Podemos parametrizar x e y apenas, que ai z vai estar em função de x mesmo pela equação do plano! Assim olha

x = r cos ⁡ t

y = r sen ⁡ t

z = 4 - r cos ⁡ t ⏟ 4 - x

Os limites novamente podem ser dados pelo círculo x 2 + y 2 = 1 , vão ser os mesmos da superfície anterior

0 ≤ r ≤ 1

0 ≤ θ ≤ 2 π

O vetor normal vai ser calculado pelas derivadas

∂ φ ∂ r = cos ⁡ t , sen ⁡ t , - cos ⁡ t

∂ φ ∂ t = - r sen ⁡ t , r cos ⁡ t ,   r sen ⁡ t

N → = i j k cos ⁡ t sen ⁡ t - cos ⁡ t - r sen ⁡ t r cos ⁡ t r sen ⁡ t

= r sen 2 ⁡ t + r cos 2 ⁡ t , r sen ⁡ t cos ⁡ t - r sen ⁡ t cos ⁡ t , r cos 2 ⁡ t + r sen 2 ⁡ t

N → = r , 0 , r

N → = r 2 + r 2 = 2 r

Passo 7

Substituindo tudo na integral

∬ S I I I z d S = ∫ 0 2 π ∫ 0 1 4 - r cos ⁡ t 2 r d r d t

= 2 ∫ 0 2 π ∫ 0 1 4 r - r 2 cos ⁡ t d r d t

= 2 ∫ 0 2 π 4 r 2 2 - r 3 cos ⁡ t 3   r = 0 r = 1 d t = 2 ∫ 0 2 π 2 - cos ⁡ t 3 d t

= 2 2 t - sen ⁡ t 3 t = 0 t = 2 π

Aqui os dois senos vão valer zero, portanto a integral fica

= 2 4 π = 4 2 π

Passo 8

Pronto! Agora somando todas as integrais das três superfícies

∬ S f ( x , y , z ) d S = ∬ S I f ( x , y , z ) d S + ∬ S I I f ( x , y , z ) d S + ∬ S I I I f ( x , y , z ) d S

∬ S f x , y , z d S = 31 π 2 + π + 4 2 π

∬ S f ( x , y , z ) d S = 4 2 + 33 2 π

Resposta

4 2 + 33 2 π

Exercícios de Livros Relacionados

Encontre a área da superfície com precisão de quatro casas decimais, expressando-a em termos de uma integral unidimensional e usando sua calculadora para estimar a integral.A Parte da superfície z = c
Calcule a integral de superfície. ∬ x 2 y z d S S é a parte do plano z = 1 + 2 x + 3 y que está acima do retângulo 0,3 × 0,2 .
Determine a área da superfície.A parte do cone z = x 2 + y 2 que se encontra entre o plano y = x e o cilindro y = x 2 .
Encontre a área da superfície com precisão de quatro casas decimais, expressando-a em termos de um a integral unidimensional e usando sua calculadora para estimar a integral.A Parte da superfície z =
Calcule a integral de superfície. ∬ x 2 + y 2 d S , S é a superfície com equação vetorial. r u , v =2 u v , u 2 - v 2, u 2 + v 2, u 2 + v 2 ≤ 1