8) O cilindro divide a esfera em duas regiões e , onde está no interior do cilindro e fora. Ache a razão das áreas .
Passo 1
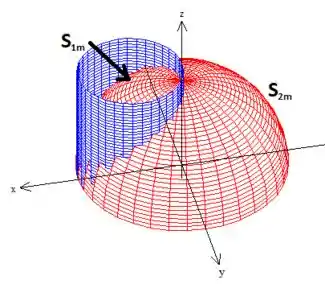
Bem, primeiro vamos entender aqui quem são essas superfícies e desenhando:
Sabemos que temos um cilindro deslocado em , pois se completarmos quadrado...
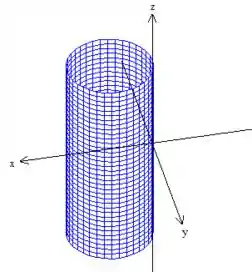
Um cilindro deslodado meia unidade em e de raio :
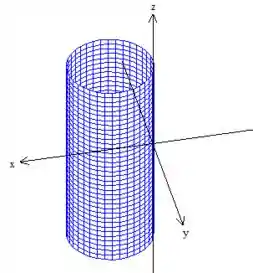
Além disso, temos a esfera de raio :
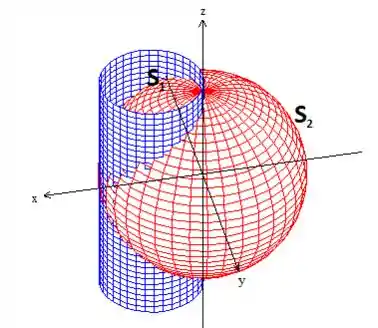
Observe que o cilindro delimita dentro dele dois pedaços da esfera que o problema informou ser enquanto é todo o resto da esfera.
Passo 2
Observe que as superfícies têm uma simetria em relação ao plano , como se pudéssemos quebra-la ao meio e a parte de baixo seria o reflexo da de cima:
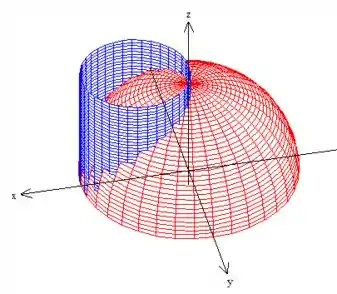
Como o problema nos pediu razão entre a área do interior ao cilindro pela área do pedaço exterior, o fato de ser simétrica implica diretamente que podemos fazer essa razão apenas com essa parte metade de cima, que será exatamente a mesma razão caso pegássemos todo o globo!
Esse pensamento já simplifica em... Nem sei quantificar, mas sei que simplifica muito.
Falando isso que acabamos de falar de uma forma mais matemática, se for a parte de da metade do globo fora ao cilindro e , a penas o pedaço de cima, mas dentro do cilindro, então:
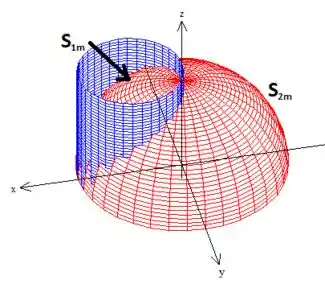
Passo 3
Bem, a área que está fora do cilindro nessa metade que estamos trabalhando nada mais é do que a área de uma semiesfera de raio ...
menos a área que está na parte de dentro...
Sendo assim, a razão que queremos fica...
Pow, então o que precisamos saber na realidade é qual é a área de , ou melhor, a área da parte de cima da região delimitada pelo cilindro...
Vamos calcular?
Passo 4
Então, área de superfície para nós a parir deste momento será dado por uma integral de superfície escalar bem especial. Essa daqui, oh:
Como toda e boa integral de superfície escalar vamos seguir um passo a passo maroto que nos ajudará muito:
1º - Parametrizar a superfície .
2º - Encontrar o termo .
Passo 5
Precisamos da superfície parametrizada. Como queremos um pedacinho da parte de cima da esfera de equação
Isolando o ...
Podemos pensar em uma parametrização explícita, tal que os dois parâmetros sejam o próprio e ...
Passo 6
Como toda e qualquer parametrização, necessitamos de determinar onde é que os parâmetros e estão variando.
Bem, e varia na limitação do cilindro deslocado...
Como se olhássemos de cima para baixo:
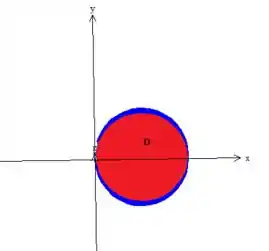
Por hora, podemos simplesmente indicar que e estão dentro dessa região aí, apenas para não perder o foco na integral de superfície ;)
Passo 7
Beleza, então com essa primeira etapa já resolvida podemos sair em busca do termo ...
Onde esse vetor normal é dado por...
Mas como parametrizamos como em função explícita de e , ou melhor, como um gráfico de função, podemos usar o bizu de vetor normal nessas condições e ganhar tempo...
como
Então...
Calculando o módulo...
Passo 8
Voltando para integral de linha que estamos resolvendo...
E substituindo esses termos que determinamos (lembrando que , trocamos por que é a região de variação de e ).
Agora assim, estamos lidando com uma integral dupla envolvendo coisas ao quadrado, podemos pensar nas mudanças para coordenadas polares...
Passo 9
Para os limites de e de , olhemos novamente para a região de variação de e :
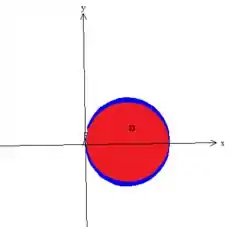
Note que que com essa substituição sai do eixo girando no sentido anti-horário, tem que variar nesse caso de até ...
Enquanto isso o varia de até a circunferência do cilindro deslocado...
Substituindo...
Fazendo uma mudança...
E não se esquecendo de também de trocar os limites de integração...
Substituindo-se na integral dupla...
Passo 10
Voltando para a razão que queremos saber definida lá no passo ...