Calcule a integral de superfície , onde é a parte do elipsóide contida no semi-espaço .
Passo 1
é isso aqui:
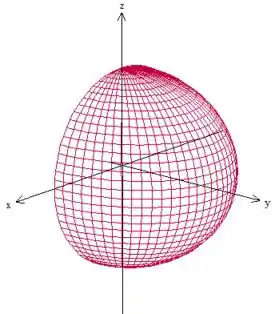
Beleza?
Como é um elipsoide, vamos fazer a parametrização em coordenadas esféricas (com os coeficientes do elipsoide):
Como , vemos pela figura, que . Temos também . É, só que temos um problema.
Quando a gente calcula a normal a uma esfera em coordenadas esféricas, se você se lembrar, vamos formando identidades e simplificando a expressão.
Só que, quando nós colocamos esses coeficientes na mudança esférica, não podemos fazer isso. Pelo menos, não simplificar tanto. Aí o problema cai em uma integral meio impossível (pode tentar).
Isso acontece porque as coordenadas esféricas são definidas com simetria em relação ao eixo , ou seja, em geral, a região que tem simetria em relação a esse eixo fica bem escrita nessas coordenadas (cones, esferas, etc). Acontece que esse elipsoide não tem essa simetria: ele é deformado na direção (é a variável com coeficiente diferente).
Bem, se ele é deformado nessa direção, quer dizer que ele tem simetria em relação a esse eixo né? Então, vamos fazer o eixo “virar” o nosso novo eixo :
A gente “desceu” e uma linha na mudança esférica. Agora tem a definição que em geral damos para . Faltam os coeficientes, né?
Beleza? Isso nos dá essa parametrização aqui:
Onde e . Lembre-se de que o ângulo é marcado no plano e em relação a .
Passo 2
Temos uma integral de superfície escalar, então precisamos achar a norma do vetor normal, primeiro vamos achar o vetor normal, ele vai ser
Vamos começar achando as derivadas da parametrização
O vetor normal vai ser
Passo 3
A normal vai ficar
Passo 4
A integral vai ficar
O que nos dá
Passo 5
Agora temos que resolver isso aí:
Agora fazemos a substituição:
Usando a relação
Lembrando que
Agora precisamos achar esses limites de integração, lembrando que tínhamos
Onde
ACABAMOSSS!