Calcule a área da parte superior da esfera contida no interior do cilindro .

Agora temos que limitar a nossa região de integração. Sabemos que a esfera está no interior do cilindro:

Apesar de que não sabemos como desenhar essa forma bizarra, o fato é que já temos uma parametrização para e , portanto podemos substituí-la para ver se ajuda na nossa análise. Nós chegamos anteriormente que:

Repare: Ao substituirmos a nossa parametrização da esfera na equação do cilindro, estamos averiguando os valores de e de para os quais a esfera e o cilindro são iguais, ou seja, onde os gráficos se encontram, e não onde na esfera estamos dentro do cilindro (que é o que o enunciado pede).

Substituindo:

Arrumando:

Utilizando a relação de soma de arcos:

Não podemos dividir ambos os lados por pois esse valor pode ser igual à zero, dependendo de . Vamos então tentar resolver:

Pronto. Os nossos limites de integração tem que sair da análise que vamos fazer da equação acima.

Como a esfera encontra com o cilindro quando essa equação acima é satisfeita, ela encontra quando ou quando .

Como sabemos que o ângulo , por definição, pertence ao intervalo , sabemos que o seu seno não pode assumir valores negativos como . Logo, é razoável assumir que os pontos da esfera que estão dentro do cilindro respeitam esta relação:

E o ? Como fica? Normalmente deixamos ele assumir qualquer valor, mas vamos ver se isto é valido neste caso. Olhando a equação abaixo percebemos uma coisa peculiar:

As duas variáveis são independentes. O que significa que o pode assumir valores diferentes de zero, independentemente do . Portanto, se tivermos:

Podemos dividir ambos os lados da equação por que não tem problema. Neste caso, observamos:

Ou seja, aqui fica mais claro uma coisa com relação à . O lado esquerdo da equação acima é um quadrado perfeito, portanto sempre positivo. Ao passo que o lado direito poderia assumir valores negativos. Não podemos deixar isto acontecer, para que a equação tenha sentido. Portanto:

Como estipulamos que está no intervalo , portanto está em , logo os valores que satisfazem esta equação neste intervalo são:

Dividindo por dois as inequações, temos que o intervalo ao qual pertence é:

Portanto, o nosso domínio de integração vai ser:

Aplicando a fórmula da integral de superfície:

Já sabemos quanto dá esse vetor normal da esfera, mas por prática nós vamos calcular tudo, começando pelas derivadas parciais:

Calculando o produto vetorial:

Fica uma dica aqui: você pode fatorar do determinante do produto vetorial um termo de uma linha ou coluna dele. No caso nunca vamos fatorar as colunas porque o primeiro elemento é sempre um vetor (), mas de resto esse truque é bastante útil. Na última linha podemos fatorar o :

Pra quem acha que vai ajudar também pode fatorar da segunda linha o , lembrando que vai sobrar na última coluna. Eu não acho tão útil assim porque pode confundir mais depois, mas fica à critério de cada um. Seguindo:

Fazendo a distributiva do que nós pusemos em evidência lá em cima:

Buscando o módulo dessa monstruosidade:

It’s Algebra Time, baby! Pondo em evidência:

Pondo em evidência:

Como o ângulo , por definição, pertence ao intervalo ele nunca é negativo, portanto:

Finalmente, podemos plugar os valores dos limites de integração na fórmula. Lembrando que os valores de se encontram numa união de intervalos, então teríamos que fazer quatro integrais (que vão dar a mesma coisa no final...). Aproveitando a simetria do problema, podemos simplesmente usar apenas um intervalo e multiplicar a integral por quatro. Plugando:

Integrando o seno obtemos:

Aplicando com os valores de integração:

Essa bagunça de cosseno do arco seno pode ser resolvida da seguinte maneira. Forçando a existência de um triângulo de hipotenusa e cateto oposto igual à :

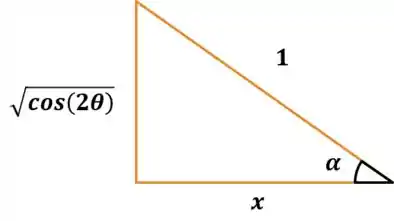
O ângulo é o arco cujo seno é , logo ele é . O que queremos é o seu cosseno:

Plugando na outra integral:

Arrumando essa raiz de cosseno de :

Plugando na expressão problemática:

Cuidado quando for tirar o seno ao quadrado da raiz, pois ele poderia admitir valores negativos, portanto tem que ser o módulo:

Felizmente no intervalo que estamos integrando o seno é sempre positivo. Logo:

Prosseguindo:

Depois dessa Odisseia, encerramos a questão. É isso aí meu amigo. Valar Calculis: Todos os Cálculos tem que morrer!