Determine a área da parte do paraboloide hiperbólico que está entre os cilindros e
Passo 1
A superfície S é descrita como f(x,y) como dominío
Com isso podemos parametrizar por:
Note que Nesse caso particular, existe uma forma mais simples de escrever o vetor normal.
Caso não tivéssemos caído nesse caso específico, deveríamos calcular o vetor normal o jeito usualcalculando o produto vetorial com determinantes.
Passo 2
A área de S é dada por:
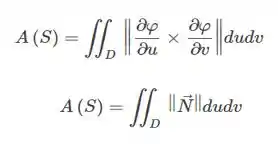
Passo 3
Vamos usar coordenadas polares para as substituições:
Substituindo nos cilindros:
Então, r varia entre 1 e 2, e dando a volta completa vai de .
Passo 4
Bora escrever nossa integral final então, sem esquecer o Jacobiano:
Substituindo por p:
Substituindo 1+p por s:
Resposta
Exercícios de Livros Relacionados
Encontre a área da superfície com precisão de quatro casas decimais, expressando-a em termos de uma integral unidimensional e usando sua calculadora para estimar a integral.A Parte da superfície z = c
Calcule a integral de superfície. ∬ x 2 y z d S S é a parte do plano z = 1 + 2 x + 3 y que está acima do retângulo 0,3 × 0,2 .
Determine a área da superfície.A parte do cone z = x 2 + y 2 que se encontra entre o plano y = x e o cilindro y = x 2 .
Encontre a área da superfície com precisão de quatro casas decimais, expressando-a em termos de um a integral unidimensional e usando sua calculadora para estimar a integral.A Parte da superfície z =
Calcule a integral de superfície. ∬ x 2 + y 2 d S , S é a superfície com equação vetorial. r u , v =2 u v , u 2 - v 2, u 2 + v 2, u 2 + v 2 ≤ 1