Seja S a parte da superfície de equação acima do triangulo de vértices (0,0), (1,1), (0,1).
(2.1) Encontre uma parametrização para S e determine o elemento de superfície dS de S. Explicite o domínio da parametrização em termos das coordenadas.
(2.2)Calcule a integral de superfície.
Passo 1
Para encontrar a parametrização de S, vamos fazer uma parametrização explicita, onde ficamos com:
Analisando agora o domínio. Observe que o enunciado nos informa que está acima do triangulo de vértices (0,0), (1,1), (0,1), ou seja:
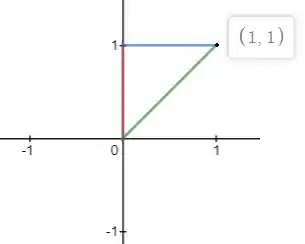
Então vamor ter de descobrir a equação de cada uma dessas retas. As retas azul (paralela ao eixo x) e vermelha (em cima do eixo y) são mais simples de encontrar a equação, ficando com y=1 e x=0 respectivamente.
Para a reta verde teremos:
Agora podemos então escrever observando o gráfico:
Passo 2
(2.2) Calcule a integral de superfície.
Escrevendo esse campo em função da parametrização ficamos com:
Então a integral fica: