UTFPR. Calculo Avançado. Lista 2 de Exercícios - Cálculo Vetorial. AV1. Questão 1c.
1. Calcule a integral de superfície:
c) , é o hemisfério , .
Passo 1
Iae, meus queridos! Está com dificuldades nessa questão? Não se preocupe! Estamos aqui para ajudar 😉
Nessa questão, temos um caso escalar de integral de superfície onde nossa superfície é dada pela equação porém para quando .
Já sabe o que fazer nesses casos?? 🤔🤔
A princípio, nós vamos parametrizar a região , implementar a parametrização
às variáveis da função de integração e obter o modulo do vetor normal a . A partir daí, definimos os limites de integração com base na nossa parametrização.
O vetor normal a é obtido quando parametrizamos a superfície e derivamos a parametrização.
Podemos começar a partir daqui! O que acha? 😁
Passo 2
A equação que define nossa superfície é , ou seja, uma esfera de raio . Se a gente definir como , como e como lembrando lá de coordenadas esféricas
Logo, nossa parametrização é
Derivando essa parametrização com relação a , temos
Pelo teorema fundamental do cálculo, lembramos que a derivada do é e a derivada do é . Logo
Juntando essas informações, temos que a derivada de com relação a é
Agora vamos derivar com relação a . Lembrando das mesmas relações das derivadas do teorema fundamental do calculo
Derivando a primeira coordenada
A segunda coordenada
Na terceira coordenada como não temos
Ou seja
Tranquilo até aqui? 👀
Passo 3
O vetor normal a é justamente o produto vetorial entre e .
Calculando esse determinante, temos
Podemos reescreve-lo como
Colocando em evidencia no ultimo termo, temos
Sabemos que , logo reescrevemos como
Calculando o modulo desse vetor, temos
Muito grande, não é? Vamos ver se podemos diminuir um pouco
Colocando em evidencia nos dois primeiros termos
Como sabemos que , temos
Podemos colocar em evidência, veja só
Novamente lembramos da relação
Simplificando o resultado
Estava assustador no início, não é? Agora encontramos um termo bem pequeno para trabalhar!
Passo 4
Convertendo as coordenadas da função de integração para a as coordenadas da parametrização , temos
Desenvolvendo os quadrados, temos
Que tal a gente colocar em evidência? Veja só
Como , logo
O que resta é obter os limites de integração para e .
Lembra lá das coordenadas esféricas?
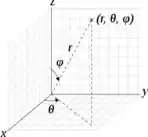
é o ângulo com relação ao semieixo positivo e é o ângulo em relação ao semieixo positivo que a superfície existe.
Como nossa superfície é uma semiesfera centrada na origem, dá toda a volta no plano , logo varia de a !
Para , foi dito no enunciado que estamos interessados apenas em , ou seja, a parte de cima da esfera, logo vemos que varia entre e .
Logo, os limites de integração para e são
Com esses resultados que obtemos, nossa integral será
Estamos chegando na reta final! 🤩
Está acompanhando?
Passo 5
Podemos iniciar os cálculos da nossa integral!
Organizando um pouquinho mais, temos
Vamos começar integrando com relação a
Aplicando o método de substituição fazendo e , ou seja
Pelo método de integração polinomial, temos
Voltando para
Aplicando os limites de integração
Agora com base nesse resultado, integramos com relação a
Como nossa função de integração é uma constante, sabemos que a integral de uma constante é a própria constante multiplicada pela variável de integração!
Aplicando os limites de integração
Com isso, chegamos a conclusão de que a integral de superfície dada no enunciado é igual a !
É isso, espero ter ajudado! Entendeu tudo? Responde Aí! 😎👍
