Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Caso Escalar

Ver Teoria
Exercício 561234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545557585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Questão 2) Calcule a integral de superfície

∬ S   x y z   d S

onde S é a parte do plano x + y + z = 1 que está no primeiro octante.

Passo 1

Estamos lidando nesse caso com uma integral de linha no caso escalar onde para resolver, seguiremos o passo a passo para a sua solução direta:

1º - Parametrizar a superfície S .

2º - Substituir os termos da parametrização na função f x ,   y ,   z .

3º - Encontrar o termo d S .

Partiu chegar ao nosso objetivo?

Passo 2

Bem, primeiro, como vimos, devemos parametrizar a superfície S . Porém, Quem é essa superfície? Como o próprio exercício nos indicou é o plano que passa pelos pontos...

1 ,   0 ,   0 , 0 ,   1 ,   0   e   0 ,   0 ,   1

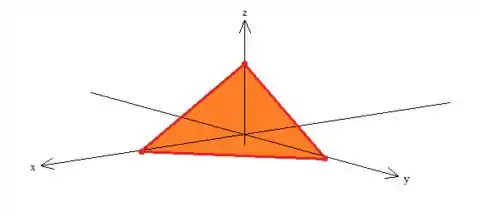
Passo 3

Parametrizar um plano, que tem uma equação explícita, pode ser feito utilizando a parametrização explícita...

                                          x = u

                                            y = v

x + y + z = 1       →       z = 1 - u - v

Com uma notação um pouco mais gentil...

r → u ,   v = u ,   v ,   1 - u - v

Passo 4

Mas não se esqueça de informar à região que e as novas variáveis variam. No caso, como u e v , são x e y , nada mais justo que olhar para a projeção (sombra ou visão de cima) da superfície no plano x y ...

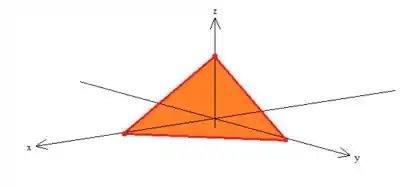
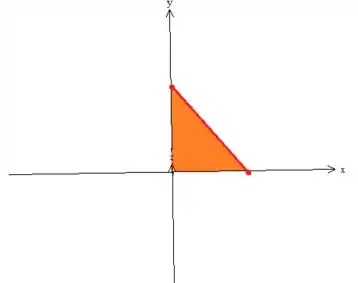
Podemos descrever essa região como do sendo do Tipo 1 , pois y , ou melhor, v varia de zero a até a reta vermelho escuro. Note que essa reta acontece quando o plano passa por z = 0 ...

x + y + z = 1     →         x + y = 1   →         y = 1 - x     →

v = 1 - u

Logo...

0 ≤ v ≤ 1 - u

Enquanto o u , varia de 0 até ao ponto de encontro dessa reta com o eixo u ...

1 - u = 0     →           u = 1

0 ≤ u ≤ 1

Passo 5

Então, agora precisamos substituir os termos da função que estamos integrando...

f x ,   y ,   z = x y z

Pelos termos da parametrização...

x = u

y = v

z = 1 - u - v

Logo...

f x ,   y ,   z = x y z         →             f r → u ,   v = u v 1 - u - v →

f r → u ,   v = u v - u 2 v - u v 2

Passo 6

Beleza, então com essas etapas concluídas, podemos sair em busca do termo d S ...

d S = N →   d u d v

Onde esse vetor normal é dado por...

N → = ∂ r → u ,   v ∂ u × ∂ r → u ,   v ∂ v

Mas como estamos utilizando uma parametrização como gráfico de função...

z = 1 - u - v

Podemos calcular N → pelo bizu...

N → = - ∂ z ∂ u ,   - ∂ z ∂ v , 1

Então

N → = 1 ,   1 ,   1

Extraindo o módulo...

N → = 1 2 + 1 2 + 1 2   →

N → = 3

Então...

d S = 3   d u d v

Passo 7

Voltando para integral de linha que estamos resolvendo...

∬ S   f x ,   y ,   z d S

E substituindo esses termos que determinamos (lembrando que S , trocamos por D que é a região de variação de u e v ).

∬ S   f x ,   y ,   z d S = ∬ D   u v - u 2 v - u v 2   3   d u d v =

3 ∫ 0 1 ∫ 0 1 - u u v - u 2 v - u v 2   d v d u

Calculando essa integral dupla considerando a u como constante...

3 ∫ 0 1 ∫ 0 1 - u   u v - u 2 v - u v 2 d v d u =

3 ∫ 0 1 u ⋅ v 2 2 - u 2 ⋅ v 2 2 - u ⋅ v 3 3 0 1 - u d u =

Substituindo os limites em v , pois foi ele quem integramos...

3 ∫ 0 1 u ⋅ 1 - u 2 2 - u 2 ⋅ 1 - u 2 2 - u ⋅ 1 - u 3 3 d u =

E simplificando um pouco...

3 ∫ 0 1 u ⋅ 1 - u 2 2 1 - u - u ⋅ 1 - u 3 3 d u =

3 ∫ 0 1 u ⋅ 3 1 - u 3 6 - u ⋅ 2 1 - u 3 6 d u =

3 ∫ 0 1 u 6 1 - u 3 d u =

3 6 ∫ 0 1 u 1 - 3 u + 3 u 2 - u 3 d u =

3 6 ∫ 0 1 u - 3 u 2 + 3 u 3 - u 4 d u =

3 6 u 2 2 - u 3 + 3 u 4 4 - u 5 5 0 1 =

3 6 1 2 - 1 + 3 4 - 1 5 = 3 6 1 20

Então...

∬ S   f x ,   y ,   z d S = 3 120

Resposta

3 120

Exercícios de Livros Relacionados

Encontre a área da superfície com precisão de quatro casas decimais, expressando-a em termos de uma integral unidimensional e usando sua calculadora para estimar a integral.A Parte da superfície z = c
Calcule a integral de superfície. ∬ x 2 y z d S S é a parte do plano z = 1 + 2 x + 3 y que está acima do retângulo 0,3 × 0,2 .
Determine a área da superfície.A parte do cone z = x 2 + y 2 que se encontra entre o plano y = x e o cilindro y = x 2 .
Encontre a área da superfície com precisão de quatro casas decimais, expressando-a em termos de um a integral unidimensional e usando sua calculadora para estimar a integral.A Parte da superfície z =
Calcule a integral de superfície. ∬ x 2 + y 2 d S , S é a superfície com equação vetorial. r u , v =2 u v , u 2 - v 2, u 2 + v 2, u 2 + v 2 ≤ 1