(2) O valor da integral da função escalar sobre a superfície é:
Passo 1
Montemos primeiro a integral que o problema quer que calculemos e como ele quer uma integral de uma função escalar sobre uma superfície, só pode ser uma integral de superfície escalar !
Como toda e boa integral de superfície seguiremos um passo a passo:
- Parametrizar a superfície pedida no problema
- Encontrar o termo
- Substituir os termos da parametrização em
E aí? Bora? :D
Passo 2
Precisamos parametrizar a superfície que queremos a área, mas por falar nisso, quem é essa superfície?
Bem, basta seguir o enunciado que indica que estamos sob um pedacinho de cilindro ao redor de , só que acima do plano :
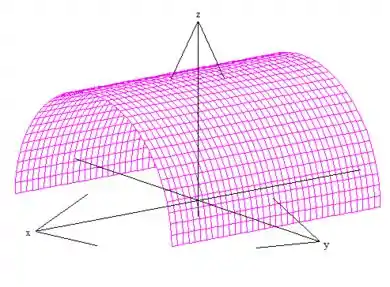
Parametrizar esse pedacinho de cilindro pode ser feito utilizando as primas das coordenadas cilíndricas:
Porém com duas diferenças:
1º é que com essa parametrização, estaríamos ao redor de , como não é verdade, trocamos por :
2º é que aqui não podemos ter três incógnitas (uma superfície só tem ), por isso desaparece e vira o raio do cilindro que é :
E a parametrização final é:
Como está no plano agora, e, além disso, o cosseno é o , começa a girar saindo do e no sentido anti-horário...
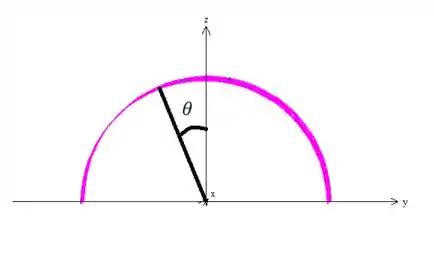
Então no nosso caso, o tem que sair do e ira até saca?
e varia de até (Pelo próprio enunciado)
Passo 3
Para encontrar o termo basta que apliquemos a fórmula:
Onde esse vetor norma ...
Como , podemos calcular essas derivadas parciais:
Um produto vetorial é dado pelo determinando dos vetores calculados...
Calculando esse determinante:
Logo, o vetor normal é:
Toda superfície tem dois vetores normais: esse e a versão negativa desse. Para nós, isso não interessa, pois queremos o módulo:
Portanto:
Passo 4
Substituindo também a função pelos termos da parametrização ganhamos...
Voltando então para a integral e substituindo tudo...
Resolvendo a integral dupla...