Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Caso Escalar

Ver Teoria
Exercício 561234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545557585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Questão 1) Seja S a superfície da esfera x 2 + y 2 + z 2 = 4 que está dentro do cone

z = x 2 + y 2 3

  1. Esboce a superfície S .
  2. Parametrize a superfície.
  3. Determine o vetor unitário no ponto 0 ,   2 ,   2 que aponta para baixo.
  4. Calcule a área de S .

Passo 1

a )

Para começar o desenho da região, vamos por partes aqui:

1º desenhamos a esfera de raio 2 e centrada na origem e também devemos desenhar o cone cortando a esfera:

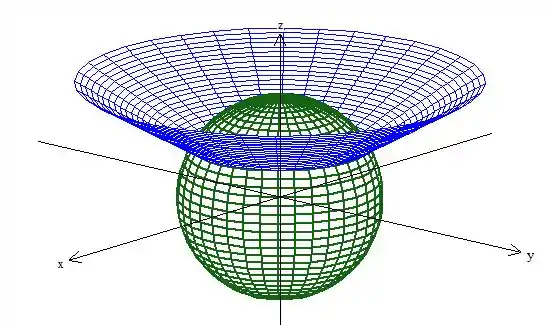
Então a superfície que buscamos trabalhar é essa daqui oh:

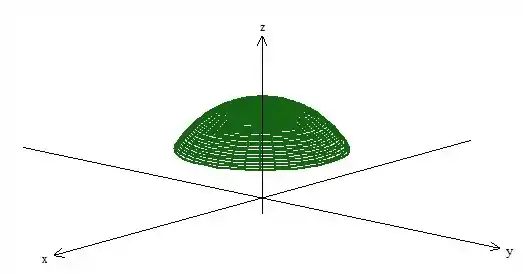
(um pedaço de esfera dentro de um cone ;)

Passo 2

b )

Como se trata de uma esfera, podemos utilizar as parametrizações esféricas:

x = R sin ⁡ φ cos ⁡ θ

y = R sin ⁡ φ sin ⁡ θ

z = R cos ⁡ φ

Mas veja que em uma superfície apenas 2 parâmetros são necessários para descrevê-la. Porém não tem problema algum aqui, pois R não é um parâmetro... Ele é o raio da esfera R = 2 , saca?

x = 2 sin ⁡ φ cos ⁡ θ

y = 2 sin ⁡ φ sin ⁡ θ

z = 2 cos ⁡ φ

Logo, a parametrização em termos de φ e θ é...

σ θ ,   φ = 2 sin ⁡ φ cos ⁡ θ , 2 sin ⁡ φ sin ⁡ θ , 2 cos ⁡ φ  

Passo 3

Bem, mas agora veja: nunca você deve sair de uma parametrização sem antes dizer onde seus parâmetros estão variando!

No caso da parametrização esférica basta lembrarmos onde os parâmetros variam:

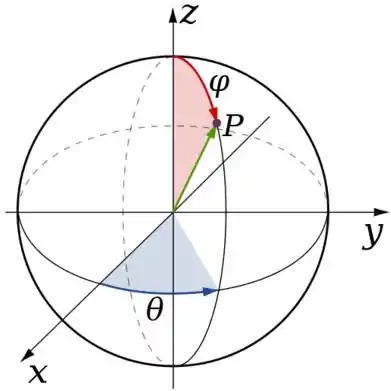
Isso nos diz que θ vai dar uma volta inteira

θ ∈ 0,2 π

O que está sendo limitado é φ pelo encontro do cone com a esfera. Para encontrar esse encontro matematicamente falando (que é o que agente quer) basta resolvermos o sistema com a equação dos dois:

x 2 + y 2 3   x 2 + y 2 + z 2 = 4

Então...

  z = x 2 + y 2 3

3 z 2 = x 2 + y 2

Substituindo isso na equação da esfera vamos ter

x 2 + y 2 + z 2 = 4

3 z 2 + z 2 = 4

4 z 2 = 4

z 2 = 1

z = 1

Estamos pegando o valor positivo de z porque z > 0 por ser uma raiz positiva.

Usando as coordenadas esféricas vamos ter

2 cos ⁡ φ = 1

cos ⁡ φ = 1 2

O ângulo que tem cosseno igual a 1 2 é 60 ° que vai ser, em radianos,

φ = π 3

Então vamos ter

φ ∈ 0 , π 3

Passo 4

c )

Para determinar qualquer vetor normal à superfície, o que devemos fazer é calcular pela fórmula

N → = ∂ σ ( φ , θ ) ∂ φ × ∂ σ ( φ , θ ) ∂ θ

Sendo

σ θ ,   φ = 2 sin ⁡ φ cos ⁡ θ , 2 sin ⁡ φ sin ⁡ θ , 2 cos ⁡ φ  

Então...

∂ σ ( φ , θ ) ∂ φ = 2 cos ⁡ φ cos ⁡ θ , 2 cos ⁡ φ sin ⁡ θ , - 2 sin ⁡ φ  

∂ σ ( φ , θ ) ∂ θ = - 2 sin ⁡ φ sin ⁡ θ , 2 sin ⁡ φ cos ⁡ θ , 0  

Aplicando o determinante que o produto vetorial requer...

N → = ∂ σ φ , θ ∂ φ × ∂ σ φ , θ ∂ θ =

i → j → k → 2 cos ⁡ φ cos ⁡ θ 2 cos ⁡ φ sin ⁡ θ - 2 sin ⁡ φ - 2 sin ⁡ φ sin ⁡ θ 2 sin ⁡ φ cos ⁡ θ 0 =

E resolvendo, vamos encontrar...

4 sin 2 ⁡ φ sin ⁡ θ j → + 4 sin ⁡ φ cos ⁡ φ cos 2 ⁡ θ k → - - 4 sin 2 ⁡ φ cos ⁡ θ i → - 4 sin ⁡ φ cos ⁡ φ sin 2 ⁡ θ k → =

Dando aquela simplificada:

4 sin 2 ⁡ φ cos ⁡ θ i → + 4 sin 2 ⁡ φ sin ⁡ θ j → + 4 sin ⁡ φ cos ⁡ φ cos 2 ⁡ θ + sin 2 ⁡ θ k → =

4 sin 2 ⁡ φ cos ⁡ θ i → + 4 sin 2 ⁡ φ sin ⁡ θ j → + 4 sin ⁡ φ cos ⁡ φ k →

Chegamos ao vetor normal:

N → = 4 sin 2 ⁡ φ cos ⁡ θ ,   4 sin 2 ⁡ φ sin ⁡ θ ,   4 sin ⁡ φ cos ⁡ φ

Passo 5

Chegamos a uma expressão para o vetor normal, mas precisamos encontrar um vetor normal no ponto...

  0 ,   2 ,   2

como nas mudanças temos...

x = 2 sin ⁡ φ cos ⁡ θ

y = 2 sin ⁡ φ sin ⁡ θ

z = 2 cos ⁡ φ

Temos que...

0 = 2 sin ⁡ φ cos ⁡ θ

2 = 2 sin ⁡ φ sin ⁡ θ

2 = 2 cos ⁡ φ

Para encontrar os ângulos que correspondem ao ponto dado basta resolver esse sistema:

2 = 2 cos ⁡ φ         →             cos ⁡ φ = 2 2

O ângulo correspondente é 45 ° já que φ varia de 0 a   π e nesse intervalo o cosseno só assume esse valor nesse ângulo, então

φ = π 4

Por outro lado...

0 = 2 sin ⁡ φ cos ⁡ θ     →

Sabemos que o sin ⁡ 45 °   não é 0 , então...

  cos ⁡ θ = 0

Veja que como θ varia de 0 até 2 π e nesse intervalo o θ pode ser...

θ = π 2       o u           θ = 3 π 2

Que ambos os valores 0 o cosseno, saca? Para encontrar o valor, vamos pela outra equação...

2 = 2 sin ⁡ φ sin ⁡ θ     →

sin ⁡ π 4 sin ⁡ θ = 2 2   →

2 2 sin ⁡ θ = 2 2   →

sin ⁡ θ = 1

RARA! O único θ (entre esses 2 ) que tem o seno 1 é...

θ = π 2

Com esses 2 pontos podemos localizar o vetor normal...

N → = 4 sin 2 ⁡ φ cos ⁡ θ ,   4 sin 2 ⁡ φ sin ⁡ θ ,   4 sin ⁡ φ cos ⁡ φ   →

N → = 4 sin 2 ⁡ π 4 cos ⁡ π 2 ,   4 sin 2 ⁡ π 4 sin ⁡ π 2 ,   4 sin ⁡ π 4 cos ⁡ π 4   →

N → = 4 2 2 2 ⋅ 0 ,   4 2 2 2 ⋅ 1 ,   4 ⋅ 2 2 ⋅ 2 2   →

N → = 0 ,   2 ,   2

Agora, veja que o problema quer o vetor normal apontando para baixo...

N → = 0 ,   - 2 ,   - 2

E além disso ele que apenas o vetor normal unitário...

n → = N → N → =

0 ,   - 2 ,   - 2 0 2 + - 2 2 + - 2 2 = 0 ,   - 2 8 ,   - 2 8 →

Dando só mais uma simplificada...

n → = 0 ,   - 2 2 2 ,   - 2 2 2   →     n → = 0 ,   - 2 2 ,   - 2 2

Passo 6

d )

Aplicando a fórmula da integral de superfície:

A = ∬ D   N → d φ d θ →

Calculando esse módulo aí separadamente...

N → = 4 sin 2 ⁡ φ cos ⁡ θ ,   4 sin 2 ⁡ φ sin ⁡ θ ,   4 sin ⁡ φ cos ⁡ φ

N → = 4 sin 2 ⁡ φ cos ⁡ θ 2 + 4 sin 2 ⁡ φ sin ⁡ θ 2 + 4 sin ⁡ φ cos ⁡ φ 2     →

N → = 16 sin 4 ⁡ φ cos 2 ⁡ θ + 16 sin 4 ⁡ φ sin 2 ⁡ θ + 16 sin 2 ⁡ φ cos 2 ⁡ φ     →

N → = 16 sin 4 ⁡ φ cos 2 ⁡ θ + sin 2 ⁡ θ + 16 sin 2 ⁡ φ cos 2 ⁡ φ     →

N → = 16 sin 4 ⁡ φ + 16 sin 2 ⁡ φ cos 2 ⁡ φ     →

Simplificando mais um pouco...

N → = 16 sin 2 ⁡ φ sin 2 ⁡ φ + cos 2 ⁡ φ     →

N → = 4 sin ⁡ φ

Legal neh? Então...

A = ∬ D   N → d φ d θ = ∬ D   4 sin ⁡ φ d φ d θ =

∫ 0 2 π ∫ 0 π 4 4 sin ⁡ φ d φ d θ

Passo 7

Resolvendo a integral...

∫ 0 2 π ∫ 0 π 3 4 sin ⁡ φ d φ d θ

⇒ ∫ 0 2 π - 4 cos ⁡ ϕ φ = 0 π / 3 d θ

⇒ ∫ 0 2 π - 4 cos ⁡ π 3 - - 4 cos ⁡ 0 d θ

⇒ ∫ 0 2 π - 4 1 2 - - 4 ∙ 1 d θ

⇒ ∫ 0 2 π - 2 + 4 d θ

⇒ ∫ 0 2 π 2 d θ

⇒ 2 θ θ = 0 2 π

⇒ 2 2 π - 0

A = 4 π

Resposta

a)

b) σ θ ,   φ = 2 sin ⁡ φ cos ⁡ θ , 2 sin ⁡ φ sin ⁡ θ , 2 cos ⁡ φ   ,               θ ∈ 0 ,   2 π     e     φ ∈ 0 , π 3

c)

n → = 0 ,   - 2 2 ,   - 2 2

d)

A = 4 π

Exercícios de Livros Relacionados

Encontre a área da superfície com precisão de quatro casas decimais, expressando-a em termos de uma integral unidimensional e usando sua calculadora para estimar a integral.A Parte da superfície z = c
Calcule a integral de superfície. ∬ x 2 y z d S S é a parte do plano z = 1 + 2 x + 3 y que está acima do retângulo 0,3 × 0,2 .
Determine a área da superfície.A parte do cone z = x 2 + y 2 que se encontra entre o plano y = x e o cilindro y = x 2 .
Encontre a área da superfície com precisão de quatro casas decimais, expressando-a em termos de um a integral unidimensional e usando sua calculadora para estimar a integral.A Parte da superfície z =
Calcule a integral de superfície. ∬ x 2 + y 2 d S , S é a superfície com equação vetorial. r u , v =2 u v , u 2 - v 2, u 2 + v 2, u 2 + v 2 ≤ 1