Monte, mas não calcule, uma integral iterada igual à integral dada
Onde é a porção do cilindro no primeiro octante entre os planos , , e
Passo 1
O primeiro passo é parametrizar a superfície !
Vamos dar uma olhada como é essa superfície e depois parametriza-la.
Primeiro, temos um cilindro circular. Esse círculo tem raio , então vamos ter
Mas ele disse que é limitado pelo plano e , então vamos ter que vai de à só.
Então só vamos pegar a parte do cilindro nessa faixa, que vai ficar
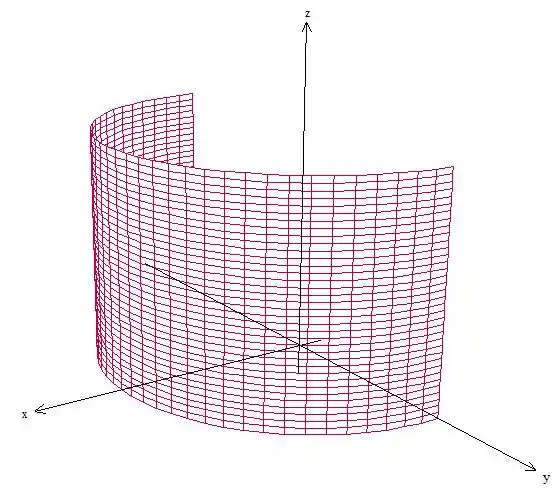
Ele também disse que vai ser limitado pelo planos e , vamos desenhar esses planos aqui
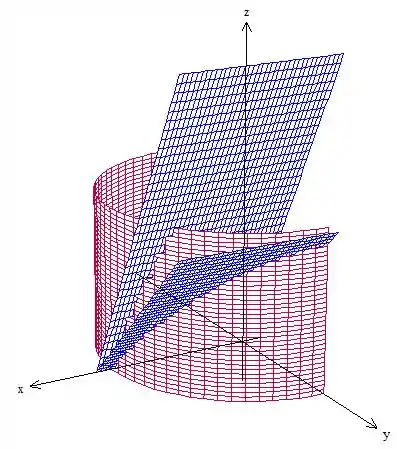
Então a nossa superfície vai ser o cilindro vermelho limitado entre esses planos azuis.
Passo 2
Vamos para a parametrização desse cilindro
Podemos parametrizar a superfície com coordenadas cilíndricas. Segue que:
Aplicando na equação do cilindro:
Portanto, o parâmetro sumiu. Até agora temos que a nossa parametrização é:
Ou seja, como é uma superfície precisamos necessariamente de dois parâmetros. Como um deles sumiu, inventamos um outro qualquer . Como se trata de um cilindro, podemos deixar o sendo o próprio parâmetro :
Logo:
E está parametrizado.
Passo 3
Agora precisamos dos limites desses parâmetros.
O enunciado nos fala que ele quer “a parte do cilindro no primeiro octante”, certo? Isso nos dá o intervalo de
Passo 4
Agora precisamos achar o intervalo de .
Repara que , então o vai estar limitado pelos planos e , ou seja,
Mas como :
Só que , então temos que:
E agora temos os dois limites da nossa parametrização, ela vai ser
Com
Passo 5
Agora que temos a parametrização, precisamos fazer a nossa integral de superfície.
Para isso precisamos achar o vetor normal , para depois pegar o módulo dele.
Lembra como faz?
Vamos fazer o nosso produto vetorial
Vamos achar essas derivadas parciais primeiro, lembrando que nossa parametrização é
Então nossas derivadas parciais são:
E
Então nosso vetor normal vai ser:
Passo 6
O módulo disso vai ficar
Passo 7
A nossa integral vai ser
Vamos trocar e pelos seus valores da parametrização
Vamos ter
Como a questão não pede pra gente resolver a integral, a resposta é isso aí =D