Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Caso Escalar

Ver Teoria
Exercício 711234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697072737475767778798081828384858687888990919293949596979899100

Enunciado

(6) Considere a , b e c tais que 0 < a < c < b . A área da parte da superfície z = c + x - a 2 + y - b 2 , z ≥ c , que fica dentro do cilindro x 2 a 2 + y 2 c 2 = 1 é:

  1. 2 π a c
  2. π a b 2
  3. π a c 2
  4. 2 π a b
  5. π a c a 2 + b 2

Passo 1

Bem, Você precisa estar consciente de que, a essa altura do campeonato, área de superfície é dada por uma integral de superfície escalar:

A = ∬ S   1   d S

E como toda integral de superfície, temos um bom passo a passo a seguir até o fim da nossa jornada:

  1. Parametrizar a superfície S pedida no problema
  2. Encontrar o termo d S

E aí? Bora? :D

Passo 2

Precisamos parametrizar a superfície que queremos a área, mas por falar nisso, quem é essa superfície?

Bem, a superfície é um cone

z = c + x - a 2 + y - b 2     →           z - c 2 = x - a 2 + y - b 2

Só que deslocado pelo ponto a ,   b ,   c ... mais ou menos, é isso aqui oh:

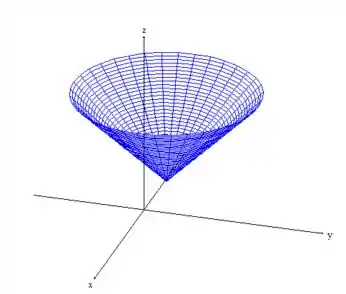
Só que queremos a parte que está dentro desse cilindro de base elíptica x 2 a 2 + y 2 c 2 = 1 :

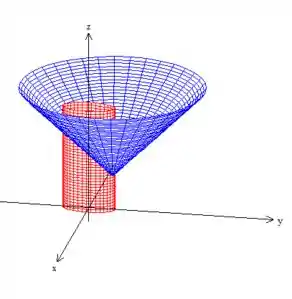
Mas é preciso que fique bem claro que a superfície é o cone e não o cilindro (o cilindro só delimita o pedaço que queremos ;D)

Passo 3

Para parametrizá-lo, como ele possui uma equação explícita em termos de x e de y ...

z = c + x - a 2 + y - b 2

Podemos parametrizar utilizando a parametrização explícita, onde o x e o y são esses parâmetros:

x = x

y = y

E

z = c + x - a 2 + y - b 2

Ou seja...

σ x ,   y = x ,   y ,   c + x - a 2 + y - b 2

Passo 4

Agora, como toda parametrização, precisamos saber onde os parâmetros, no caso o próprio x e y estão variando e é aqui que entra o cilindro!

Repare que o que delimita o x e y é justamente esse cilindro, afinal sabemos que esses parâmetros estão dentro dele:

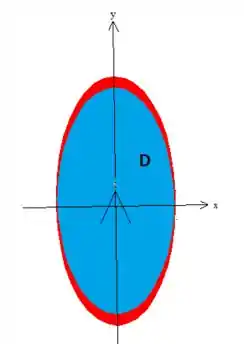
Por hora, vamos só falar que x e y estão dentro dessa região elíptica D , aí ok? Só para não perdermos o foco na resolução da integral de superfície

x ,   y ∈ D

Passo 5

Temos agora que calcular o termo   d S ...

  d S = N →   d x d y

O vetor normal, como parametrizamos explicitamente como gráfico de função ( z em função de x e y ), podemos calcula-lo utilizando o bizu:

N → = - ∂ z ∂ x ,   - ∂ z ∂ y ,   1

Como z = c + x - a 2 + y - b 2 ... Derivando (não esquecendo de aplicar a regra da cadeia)...

∂ z ∂ x = ∂ c + x - a 2 + y - b 2 ∂ x =

1 2 x - a 2 + y - b 2 ⋅ ∂ x - a 2 + y - b 2 ∂ x =

2 x - a 2 x - a 2 + y - b 2 =

x - a x - a 2 + y - b 2

Calculando a outra integral fazendo os cálculos parecidos..

∂ z ∂ y = ∂ c + x - a 2 + y - b 2 ∂ y =

1 2 x - a 2 + y - b 2 ⋅ ∂ x - a 2 + y - b 2 ∂ y =

y - b x - a 2 + y - b 2

Logo...

N → = - x - a x - a 2 + y - b 2 ,   - y - b x - a 2 + y - b 2 ,   1

O sinal não importa muito, pois o que queremos é o módulo do vetor normal:

N → = - x - a x - a 2 + y - b 2 2 + - y - b x - a 2 + y - b 2 2 + 1 2

N → = x - a 2 x - a 2 + y - b 2 + y - b 2 x - a 2 + y - b 2 + 1

N → = x - a 2 + y - b 2 x - a 2 + y - b 2 + 1

N → = 1 + 1

Então...

d S = 2 d x d y

Passo 6

Voltando para a integral que queremos resolver...

A ( S ) = ∬ S   1   d S

e substituindo o que encontramos...

A ( S ) = ∬ D   2 d x d y

Agora basta resolver a integral e correr para o abraço!

A ( S ) = 2 ∬ D   d x d y

RARA! O que é essa integral dupla aí? É área da região D ...

A S = 2 ⋅ A ( D )

Como D é conhecida, ou seja, é essa elipse...

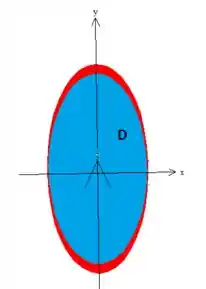
de equação x 2 a 2 + y 2 c 2 = 1 ... sua área é...

A D = a c   π

(semelhante a área da circunferência, mas troca r 2 por a c , saca?)

A S = 2 ⋅ A D =

2   a c π

Resposta

a )     2 π a c

Exercícios de Livros Relacionados

Encontre a área da superfície com precisão de quatro casas decimais, expressando-a em termos de uma integral unidimensional e usando sua calculadora para estimar a integral.A Parte da superfície z = c
Calcule a integral de superfície. ∬ x 2 y z d S S é a parte do plano z = 1 + 2 x + 3 y que está acima do retângulo 0,3 × 0,2 .
Determine a área da superfície.A parte do cone z = x 2 + y 2 que se encontra entre o plano y = x e o cilindro y = x 2 .
Encontre a área da superfície com precisão de quatro casas decimais, expressando-a em termos de um a integral unidimensional e usando sua calculadora para estimar a integral.A Parte da superfície z =
Calcule a integral de superfície. ∬ x 2 + y 2 d S , S é a superfície com equação vetorial. r u , v =2 u v , u 2 - v 2, u 2 + v 2, u 2 + v 2 ≤ 1