Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Caso Escalar

Ver Teoria
Exercício 201234567891011121314151617181921222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Calcule a integral de superfície abaixo

∬ S   x + z y + 1 2 d S ,

Onde S é a porção do cone y + 1 2 = x 2 + z 2 acima do plano z = 0 e limitada entre os planos y = 0 e y = 3 .

Passo 1

Bem, o que pretendemos aqui é encontrar o valor de uma integral de superfície no caso escalar. E para isso, o que vamos fazer basicamente é seguir o nosso famoso passo a passo para matar o nosso problema !

  1. Parametrizar a superfície S .
  2. Encontrar o termo d S .
  3. Substituir, na função do integrando, os termos da parametrização.

Então venha comigo .

Passo 2

Sabemos que a primeira coisa é parametrizar S , mas antes, acho que seria muito interessante para o nosso entendimento, conhecer a superfície primeiro (e nada melhor que alguns esboços, para conhecer uma superfície, não é não =).

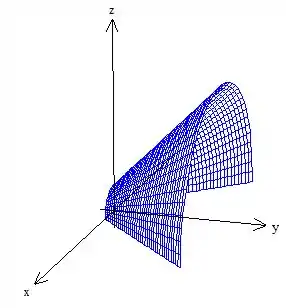
Veja que a superfície S é formada por um cone y + 1 2 = x 2 + z 2 que está girando ao redor de y e, além disso, possui vértice no ponto 0 ,   - 1 ,   0 :

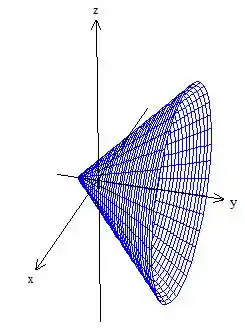
Porém o problema delimita o cone pelo chão z = 0 e também pelas paredes y = 0 e y = 3 :

Ficando como a nossa superfície S ... Prontinho!

Passo 3

Com o desenho pronto, podemos parametrizar! A boa notícia é que a parametrização pode ser feita de forma explícita, já que conseguimos explicitar uma das variáveis em função de outras duas...

y + 1 2 = x 2 + z 2             →

y + 1 = ± x 2 + z 2   →

Como y está acima de y = 0 ...

y = x 2 + z 2 - 1

Você já deve saber que toda superfície, pode é parametrizada em função de dois parâmetros independentes. Então... Os dois parâmetros nesse caso são x   e z :

σ x ,   z = x ,   x 2 + z 2 - 1 ,   z

E essa é uma boa parametrização para prosseguirmos!

Passo 4

Bem, mas você já sabe que qualquer parametrização, apenas acaba quando dizemos onde os parâmetros variam. Em nosso caso, como os parâmetros são x e z , para sabermos onde eles estão variando, sugiro fortemente olhar para a nossa superfície

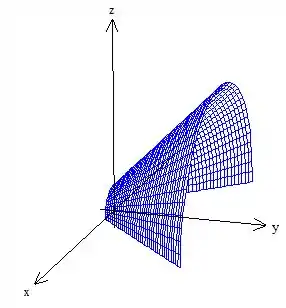
Mas dessa vez um pouco diferente: olhar para a sombra dela no plano x z , ou seja, a sua projeção:

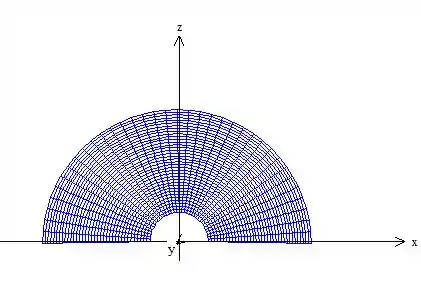
Veja que a projeção dela nesse plano é um arco e é nesse arco, que chamaremos de D , onde variam x e z ;)

Passo 5

Com a parametrização pronta, podemos mover em diante para encontrar o termo d S ...

d S = N → d x d z

Onde o vetor normal é...

N → = ∂ σ ∂ x × ∂ σ ∂ z

Calculando as derivadas parciais...

σ x ,   z = x ,   x 2 + z 2 - 1 ,   z         →             ∂ σ ∂ x = 1 , 2 x 2 x 2 + z 2 ,   0

σ x ,   z = x ,   x 2 + z 2 - 1 ,   z         →             ∂ σ ∂ z = 0 , 2 z 2 x 2 + z 2 ,   1

Como produto vetorial é um determinante, onde...

N → = i ^ j ^ k ^ 1 x x 2 + z 2 0 0 z x 2 + z 2 1 =

x x 2 + z 2 i ^ + z x 2 + z 2 k ^ - j ^

Ou

N → = x x 2 + z 2 ,   - 1 ,   z x 2 + z 2

Tirando o módulo...

N → = x x 2 + z 2 2 + - 1 2 + z x 2 + z 2 2   →

N → = x 2 x 2 + z 2 + 1 + z 2 x 2 + z 2   →

N → = x 2 + z 2 x 2 + z 2 + 1         →         N → = 1 + 1 =

N → = 2

Logo...

d S = 2 d x d z

Passo 6

Por último, antes de voltar a integral, vamos substituir a parametrização na expressão do integrando...

x + z y + 1 2

Considerando que na parametrização, a única coisa que mudou foi y = x 2 + z 2 - 1 ...

x + z y + 1 2 = x + z x 2 + z 2 - 1 + 1 2 =

x + z x 2 + z 2

Passo 7

Pow, agora é só voltar mesmo para a integral de superfície:

∬ S   x + z y + 1 2 d S

E substituir tudo o que encontramos até agora:

∬ S   x + z y + 1 2 d S = 2 ∬ D   x + z x 2 + z 2 d x d z

Daí a gente consegue ver que o que fizemos foi trocar uma integral de superfície, por uma integral dupla na região D . Como a região é um arco, podemos resolver a integral dupla, fazer uma mudança para coordenada polar:

x = r cos ⁡ θ

z = r sin ⁡ θ

J = r

A equação do círculo nos ajuda aqui também:

x 2 + z 2 = r 2

Mas veja que ainda temos um problema, onde r e θ , variam?

Passo 8

Para responder essa pergunta dê uma olhada na região D :

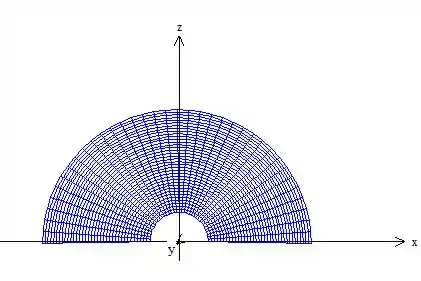
Veja que θ , está dando uma meia volta, para formar a região:

0 ≤ θ ≤ π

Enquanto r , varia entre as bordas desse anel! Como as bordas desse anel, só existem, por causa da borda da nossa superfície cônica:

Então, encontrar essas bordas é substituir na equação do cone os valores que delimita as paredes:

y + 1 2 = x 2 + z 2             p a r a   y = 0 →             x 2 + z 2 = 1

y + 1 2 = x 2 + z 2             p a r a   y = 3 →             x 2 + z 2 = 4 2

Veja que assim, temos a equação das bordas da nossa região D onde agora somos capazes de falar r varia entre...

1 ≤ r ≤ 4

Passo 9

Voltando para a integral dupla e substituindo (não se esqueça de multiplicar pelo Jacobiano):

∬ S   x + z y + 1 2 d S = 2 ∬ D   x + z x 2 + z 2 d x d z =

2 ∫ 0 π ∫ 1 4 r cos ⁡ θ + r sin ⁡ θ r 2 ⋅ J   d r d θ =

2 ∫ 0 π ∫ 1 4 r cos ⁡ θ + r sin ⁡ θ r   d r d θ =

2 ∫ 0 π ∫ 1 4 sin ⁡ θ + cos ⁡ θ   d r d θ

Agora é só integrar mesmo...

2 ∫ 0 π ∫ 1 4 sin ⁡ θ + cos ⁡ θ   d r d θ = 2 ∫ 0 π sin ⁡ θ + cos ⁡ θ ∫ 1 4   d r d θ =

2 ∫ 0 π sin ⁡ θ + cos ⁡ θ 4 - 1 d θ = 3 2 ∫ 0 π sin ⁡ θ + cos ⁡ θ d θ

3 2   - cos ⁡ θ + sin ⁡ θ   0 π =

3 2 - cos ⁡ π + sin ⁡ π - - cos ⁡ 0 + sin ⁡ 0 =

3 2 1 - - 1 = 6 2

Resposta

6 2

Exercícios de Livros Relacionados

Encontre a área da superfície com precisão de quatro casas decimais, expressando-a em termos de uma integral unidimensional e usando sua calculadora para estimar a integral.A Parte da superfície z = c
Calcule a integral de superfície. ∬ x 2 y z d S S é a parte do plano z = 1 + 2 x + 3 y que está acima do retângulo 0,3 × 0,2 .
Determine a área da superfície.A parte do cone z = x 2 + y 2 que se encontra entre o plano y = x e o cilindro y = x 2 .
Encontre a área da superfície com precisão de quatro casas decimais, expressando-a em termos de um a integral unidimensional e usando sua calculadora para estimar a integral.A Parte da superfície z =
Calcule a integral de superfície. ∬ x 2 + y 2 d S , S é a superfície com equação vetorial. r u , v =2 u v , u 2 - v 2, u 2 + v 2, u 2 + v 2 ≤ 1