Considere o cone .
a) Calcule a área da parte da superfície que se encontra no primeiro octante (ou seja, , , ) e abaixo do plano .
Passo 1
Faaaala! Podemos calcular a área de uma superfície calculando essa integral
Onde é a função que tem nossa superfície como gráfico. Repara que nossa superfície é
Mas como a gente só está em , a gente pode dizer que nossa superfície tem a equação
E essa pode então ser nossa função
Passo 2
Calculando as derivadas parciais dela
Substituindo na integral
Passo 3
Ih mas quem é ? Cara, esse é o domínio da nossa função no espaço que ele deu. Como temos uma , queremos um domínio como região do plano .
Estamos no primeiro octante, daí já temos que
Ele disse também que nossa superfície está limitada por cima pelo plano . Mas lembra que nossa superfície é
Ela é dada por , né? Então limita por cima, aí a gente pode dizer que
E isso diz para gente que temos uma região dentro de , uma circunferência de raio .
Por que? Percebe que o ponto satisfaz essa inequação, e ele está dentro da circunferência. Então realmente a gente tá olhando para essa região interior.
Vamos esboçar a região de que está dentro dessa circunferência e em e .
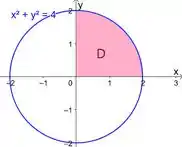
Essa região rosinha vai ser nosso domínio!
Passo 4
Agora é calcular a integral
Pensa comigo: integral dupla sobre com integrando é o mesmo que a área de . Então a gente vai escrever:
Mas quem é ? Lembra que era um quarto do círculo de raio ? Vou te mostrar ele de novo oh:
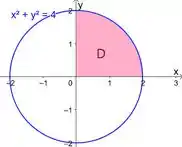
A gente pode calcular a área dele pela fórmulinha de calcular a área de um círculo:
Mas a gente quer só um quarto dessa área e :
Aí nossa área da superfície fica
Prontinho! Arrasamos!