Calcule a área da superfície da esfera de raio , centrada na origem, limitada por dois paralelos e dois meridianos, sabendo que o ângulo entre os meridianos é e a distância entre os planos que contêm os paralelos é .
Passo 1
Essa superfície foi descrita de uma forma meio diferente, né? Ele fala de meridianos e paralelos, coisa que não vimos antes. Isso vai representar aqui exatamente o que representa quando estudamos isso no ensino fundamental, os meridianos são esses aqui
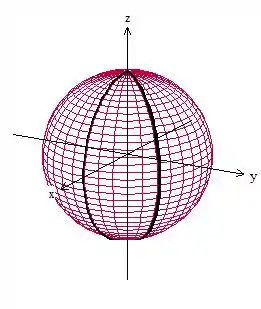
E os paralelos são esses aqui
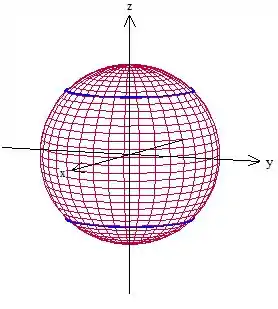
Portanto, vamos calcular a área de uma esfera normal, essa parte de paralelos e meridianos só vão servir para delimitar nossa região, beleza?
Passo 2
Vamos usar a parametrização normal da esfera de raio :
Como o ângulo entre os meridianos é , se considerarmos que começa em zero, os limites dele serão
Os paralelos vão entrar de uma forma um pouco mais diferente na conta. Perceba que no caso dos meridianos, era um ângulo, então delimitava direto. A informação dada dos paralelos é uma distância! Com isso, vamos precisar achar o ângulo associado à essa distância. Vê se fica mais claro com esses gráficos aqui
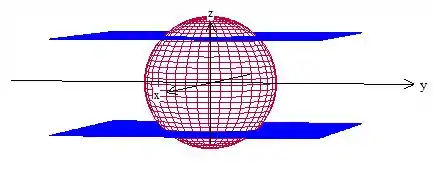
Podemos considerar os paralelos como esses planos que cortam a esfera, certo? O ângulo da origem até a interseção da esfera com os planos vão ser os limites de ! Sabemos que a distância no eixo entre os planos é , portanto, a distância da origem até um deles é
Se projetarmos esse gráfico no plano , fica assim
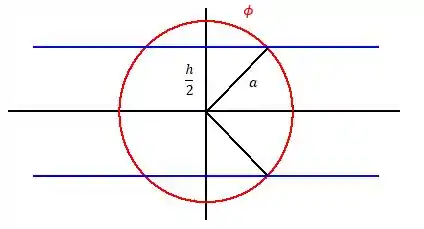
Perceba que essas linhas pretas são justamente os limites de , com essa imagem fica mais fácil relacionar com . Se pensarmos em como a altura do triangulo retângulo que possui um ângulo igual a , percebemos que
Portanto, os ângulos que vão limitar são
Essa função não é muito usada, né? Não se assuste! Ela não tem nada demais, ela só representa um ângulo que não sabemos o valor exato, mas sabemos o seu cosseno.
Passo 3
Tendo delimitado e com os paralelos e meridianos, vamos agora calcular o vetor normal para podermos integrar e descobrir a área. Sabemos que a parametrização é essa
Passo 4
Vamos tirar o módulo desse vetor
Passo 5
A integral para calcularmos a área é essa aqui
Agora é só resolver! Vamos lá
Percebe o que vai acontecer agora? Vamos fazer o cosseno do dos dois ângulos! Em outras palavras é mais ou menos isso aqui “Cosseno do arco cujo cosseno é ”, isso dá exatamente !
O mesmo se aplica ao , o resultado do cosseno desse ângulo é ! Com isso