Observe a figura abaixo que representa o toro obtido girando em torno do eixo uma circunferência com centro no ponto e com raio . A distância do ponto à origem é .
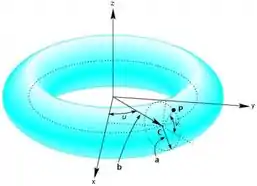
- Mostre que , é a representação paramétrica do toro, onde
- Calcule o vetor normal ao toro no ponto
- Calcule a área do toro
Passo 1
Repara que o toro nada mais é que uma superfície de revolução, ele pegou uma circunferência que está no plano com centro em com raio e racionou em torno do eixo . Lembra como fazemos uma superfície de revolução?
Primeiro vamos parametrizar a circunferência, ela tem centro em e raio então vamos ter, para a circunferência
Com
Vamos “rotacionar” isso agora, vamos ter
Então a parametrização do toro vai ficar
Com
Essa é a parametrização exatamente igual à que ele pediu.
Passo 2
Vamos agora obter o vetor normal, temos que fazer
Calculando as derivadas parciais:
Achando o produto vetorial:
Que resulta em:
Passo 3
Ele quer o vetor em , precisamos achar os valores de e que fazem chegarmos nesses pontos
Primeiro temos que
Como vamos ter
Já achamos vamos usar as outras componentes para achar
Trocando o valor de
Isso nos diz que
Assim
Vamos a última coordenada
Trocando o valor de
Isso nos diz que
Assim
Logo vamos ter
Passo 4
O vetor normal, no ponto vai ficar
Passo 5
A fórmula da área vai ser
Temos que achar a norma desse vetor normal que achamos ali em cima.
Aqui temos um problema, quando passamos a raiz temos que colocar o módulo, mas se liga numa parada
Certo? Então
Mas ele disse no início que , isso nos diz que
Então não precisamos do módulo, porque esse cara é sempre positivo.
Passo 6
Finalmente, aplicando a fórmula com os limites de integração: