Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Caso Escalar

Ver Teoria
Exercício 581234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Questão 4: Considere o corpo sólido Q no interior do cilindro x - 1 2 + y 2 = 1 , limitado por cima e por baixo pelo cone 2 x 2 + 2 y 2 - z 2 = 0 . Calcule a área de superfície de Q .

Sugestão: Evite a parametrização do cilindro como superfície de revolução com eixo deslocado!

Passo 1

Pois bem, se o problema nos pediu área de superfície isso só pode significar uma coisa: que ele nos quer avaliar se sabemos calcular uma integral de superfície escalar:

Á r e a   d e   Q = ∬ ∂ Q   1   d S

Essa é basicamente a nossa tarefa, é encontrar a superfície que delimita Q (a gente nomeia assim ∂ Q ) e calcular integrais! =)

Então bora?

Passo 2

Se vamos encontrar a área de um sólido, antes é legal a gente desenhar esse sólido, não é mesmo?

Como o próprio problema nos pediu, esse sólido é composto por um cilindro deslocado da origem em uma unidade x - 1 2 + y 2 = 1 :

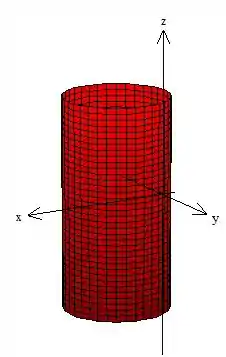
E também ele é delimitado por um cone com vértice na origem:

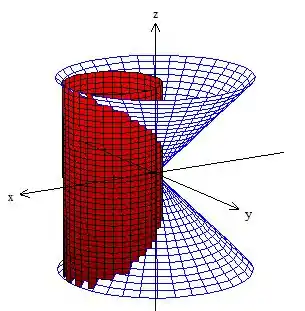
E basicamente o nosso sólido é esse camarada aí dentro dessas duas superfícies !

Acho que dá para notar que embora esse sólido tenha três superfícies delimitadoras, só precisamos calcular de duas: a da casca cilíndrica e do teto cônico, porque a área da base cônica será a mesma do teto, saca? Então se consideramos a parte cilíndrica como superfície S 1 e a parte do teto de cone como S 2 , a área total de Q será dada por...

Á r e a   d e   Q = ∬ S 1   1   d S + 2 ∬ S 2   1   d S

Passo 3

Vamos então começar pela integral de superfície do cilindro:

∬ S 1   1   d S

Vamos precisar de:

  1. Parametrizar a superfície S 1 .
  2. Encontrar o termo d S .

Para parametrizar, bem, como é um cilindro vamos parametrizar com a forma clássica (seguindo as coordenadas polares):

x = r cos ⁡ θ

y = r sin ⁡ θ

z = z

Agora, como você já sabe, uma parametrização de superfície tem que depender apenas de duas variáveis (que são os dois parâmetros). No caso do cilindro vamos ter que trocar o r . Mas agora, por qual valor vamos trocar? Vamos ver a equação novamente:

x - 1 2 + y 2 = 1

Veja que esse cilindro tem raio 1 e está deslocado em x , então, se a gente fosse utilizar parametrização com eixo deslocado, faríamos:

x = cos ⁡ θ + 1

y = sin ⁡ θ

z = z

Porém!!! O problema nos sugeriu que evitássemos essa parametrização, e eu não sei você, mas se o problema nos sugeriu, acho melhor obedecer, neh? (Mas quero deixar claro que essa parametrização não está errada).

Ok! Então qual r vamos utilizar? Bem, se substituirmos as coordenadas polares na equação do cilindro, talvez possamos ter uma resposta...

x - 1 2 + y 2 = 1               →                   x 2 - 2 x + 1 + y 2 = 1           →

x 2 + y 2 = 2 x                 →                       r cos ⁡ θ 2 + r sin ⁡ θ 2 = 2 r cos ⁡ θ

r 2 = 2   r cos ⁡ θ         →

r = 2 cos ⁡ θ

OPA!!! Então encontramos o valor de r no eixo original de coordenadas ! Assim, a nossa parametrização fica:

x = 2 cos ⁡ θ cos ⁡ θ

y = 2 cos ⁡ θ sin ⁡ θ

z = z

Ou de uma forma mais elegante:

σ θ ,   z = 2 cos ⁡ θ cos ⁡ θ ,   2 cos ⁡ θ sin ⁡ θ ,   z

Passo 4

A má notícia nesse passo é que ainda não acabou a parametrização do passo anterior, afinal de contas, o problema só acaba quando temos também os limites dos parâmetros em mãos, e é isso que vãos fazer aqui agora!

Primeiro vamos falar de θ , onde ele varia?

É importante notar das diferenças de parametrização. Se tivéssemos trabalhando com o eixo deslocado (coloquei de amarelo)...

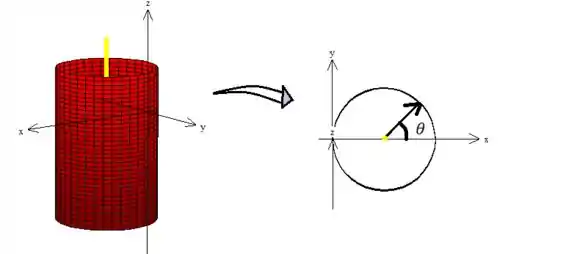
O θ estaria variando de 0 a 2 π (ou dando uma volta completa também serve).

PORÉM... Estamos trabalhando uma parametrização que não deslocou o eixo, ou seja, continuamos aqui:

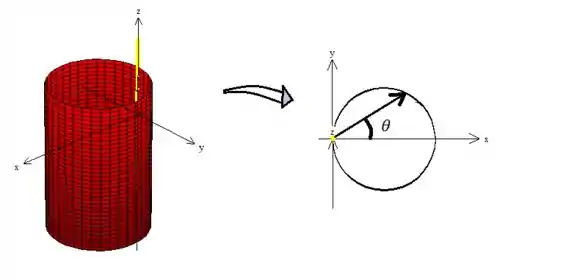
Assim... O θ no NOSSO CASO, está variando de baixo pra cima, ou seja:

- π 2 ≤ θ ≤ π 2

Já o z , bem... O cilindro está delimitado em cima e embaixo pelo cone, então basta substituir a parametrização na equação do cone:

2 x 2 + 2 y 2 - z 2 = 0         →             2 2 cos ⁡ θ cos ⁡ θ 2 + 2 2 cos ⁡ θ sin ⁡ θ 2 - z 2 = 0       →

2 4 cos 2 ⁡ θ ⋅ cos 2 ⁡ θ + 2 4 cos 2 ⁡ θ sin 2 ⁡ θ - z 2 = 0       →

8 cos 2 ⁡ θ cos 2 ⁡ θ + sin 2 ⁡ θ - z 2 = 0         →

8 cos 2 ⁡ θ = z 2         →

z = ± 2 2 cos ⁡ θ

Então...

- 2 2 cos ⁡ θ ≤ z ≤ 2 2 cos ⁡ θ

Passo 5

Com a parametrização concluída, podemos encontrar então o termo d S ...

d S = N → d z   d θ

Sendo o vetor norma determinado através da parametrização:

N → = ∂ σ ∂ θ × ∂ σ ∂ z

Como

σ θ ,   z = 2 cos ⁡ θ cos ⁡ θ ,   2 cos ⁡ θ sin ⁡ θ ,   z       →

σ θ ,   z = 2 cos 2 ⁡ θ , sin ⁡ 2 θ ,   z

Derivando...

∂ σ ∂ θ = 2 ⋅ 2 cos ⁡ θ - sin ⁡ θ , cos ⁡ 2 θ ⋅ 2 ,   0 = - 2 sin ⁡ 2 θ , 2 cos ⁡ 2 θ ,   0

∂ σ ∂ z = 0 ,   0 ,   1

E aplicando o produto vetorial...

N → = ∂ σ ∂ θ × ∂ σ ∂ z = i ^ j ^ k ^ - 2 sin ⁡ 2 θ 2 cos ⁡ 2 θ 0 0 0 1 =

2 cos ⁡ 2 θ i ^ + 2 sin ⁡ 2 θ j ^

Ou...

N → = 2 cos ⁡ 2 θ ,   2 sin ⁡ 2 θ ,   0

Extraindo o módulo...

N → = 2 cos ⁡ 2 θ 2 + 2 sin ⁡ 2 θ 2 + 0 2 =

4 cos 2 ⁡ 2 θ + 4 sin 2 ⁡ 2 θ =

4 cos 2 ⁡ 2 θ + sin 2 ⁡ 2 θ =

4 = 2

Então...

d S = 2   d z   d θ

Passo 6

Então agora podemos regressar a integral de superfície e substituir mesmo...

∬ S 1   1   d S = ∫ - π 2 π 2 ∫ - 2 2 cos ⁡ θ 2 2 cos ⁡ θ 2   d z   d θ =

2 ∫ - π 2 π 2 2 2 cos ⁡ θ - - 2 2 cos ⁡ θ d θ =

2 ∫ - π 2 π 2 4 2 cos ⁡ θ d θ = 8 2   sin ⁡ θ   - π 2 π 2 =

8 2 sin ⁡ π 2 - sin ⁡ - π 2 = 8 2 1 - - 1 =

16 2

Passo 7

ACHOU QUE ACABOU? Bem, infelizmente ainda não campeão ! Ainda falta a outra integral (a integral que calcula área da parte cônica):

∬ S 2   1   d S

Como fizemos anteriormente, precisamos:

  1. Parametrizar S 2 .
  2. Encontra d S .

Bem, agora vamos parametrizar um cone:

2 x 2 + 2 y 2 - z 2 = 0               o u                   z 2 = 2 x 2 + 2 y 2     →

z = 2 x 2 + 2 y 2

Logo, uma boa parametrização para a parte de cima do cone é:

φ x ,   y = x ,   y ,   2 x 2 + 2 y 2

Onde os parâmetros x e y estão variando? Bem, essa é mais fácil, pois só queremos o pedaço que está dentro do cilindro, ou seja:

x - 1 2 + y 2 ≤ 1

Resumindo, o x e o y , variam no disco de raio 1 que está deslocado da origem !

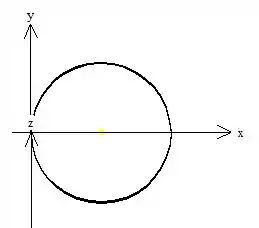
Passo 8

Para encontrar o d S dessa superfície aí, vai ser mais fácil, pois como realizamos uma parametrização como uma função de x e y , podemos utilizar o bizu para o vetor normal:

N → = - ∂ z ∂ x ,   - ∂ z ∂ y ,   1 ,             c o m o         z = 2 x 2 + 2 y 2

N → = - 1 2 2 x 2 + 2 y 2 ⋅ 4 x ,   - 1 2 2 x 2 + 2 y 2 ⋅ 4 y ,   1     →

N → = - 2 x 2 x 2 + 2 y 2 ,   - 2 y 2 x 2 + 2 y 2 ,   1

Portando o módulo será:

N → = - 2 x 2 x 2 + 2 y 2 2 + - 2 y 2 x 2 + 2 y 2 2 + 1 2   →

N → = 4 x 2 2 x 2 + 2 y 2 + 4 y 2 2 x 2 + 2 y 2 + 1     →

N → = 4 x 2 + 4 y 2 2 x 2 + 2 y 2 + 1   →

N → = 2 ( 2 x 2 + 2 y 2 ) 2 x 2 + 2 y 2 + 1   →

N → = 2 + 1 = 3

Portanto...

d S = 3   d x d y

Passo 9

Novamente retornando para o cálculo da integral de superfície:

∬ S 2   1   d S = ∬ D   3   d x d y =

3 ∬ D     d x d y

Epa!!! Essa integral dupla aí representa a área, no caso é a área da região de variação do x e y . Como a região de variação do x e y é um disco de raio 1 ...

D :           x - 1 2 + y 2 ≤ 1

Então:

∬ S 2   1   d S = 3 π 1 2 = 3 π

Passo 10

Calma, garoto! Eu sei que você está louco para terminar o problema, mas ainda temos que retornar para o que queremos desde o princípio: a área da região de Q :

Á r e a   d e   Q = ∬ S 1   1   d S + 2 ∬ S 2   1   d S     →

Á r e a   d e   Q = 16 2 + 2 3 π

Resposta

16 2 + 2 π 3

Exercícios de Livros Relacionados

Encontre a área da superfície com precisão de quatro casas decimais, expressando-a em termos de uma integral unidimensional e usando sua calculadora para estimar a integral.A Parte da superfície z = c
Calcule a integral de superfície. ∬ x 2 y z d S S é a parte do plano z = 1 + 2 x + 3 y que está acima do retângulo 0,3 × 0,2 .
Determine a área da superfície.A parte do cone z = x 2 + y 2 que se encontra entre o plano y = x e o cilindro y = x 2 .
Encontre a área da superfície com precisão de quatro casas decimais, expressando-a em termos de um a integral unidimensional e usando sua calculadora para estimar a integral.A Parte da superfície z =
Calcule a integral de superfície. ∬ x 2 + y 2 d S , S é a superfície com equação vetorial. r u , v =2 u v , u 2 - v 2, u 2 + v 2, u 2 + v 2 ≤ 1