Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Caso Escalar

Ver Teoria
Exercício 541234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Questão 3) Calcule a área da parte do paraboloide elíptico z = x 2 + 2 y 2 que se encontra dentro do cilindro 4 x 2 + 16 y 2 ≤ 1 .

Passo 1

Para fazer o cálculo dessa área, vamos precisar usar a integral de superfície descrita por

∬ S N → d S

Vamos ter que fazer bastante coisa pra chegar nessa integral certinha: primeiro vamos achar uma parametrização para a superfície, achar os seus limites e por fim o módulo do vetor normal. Quando fizermos isso, vamos voltar pra integral e resolver!

Começando pela parametrização da superfície, o esboço dela é esse aqui:

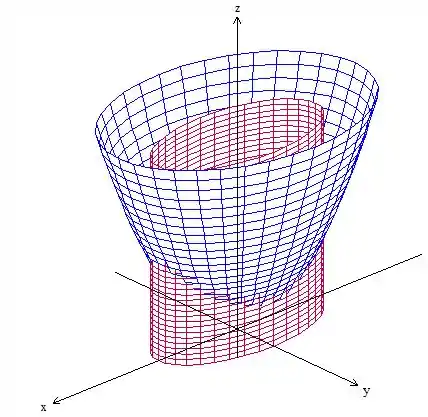
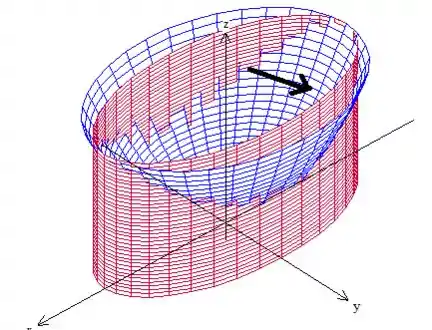
O exercício pede a superfície do paraboloide, né? Então vamos usar os cilindros somente para limitar as variáveis, a parametrização mesmo vai ser a do paraboloide. Uma possível é a seguinte:

x = x

y = y

z = x 2 + 2 y 2

Então a superfície de uma forma mais legal...

φ x ,   y = x , y ,   x 2 + 2 y 2

Passo 2

Projetando as superfícies do cilindro no plano x y fica assim

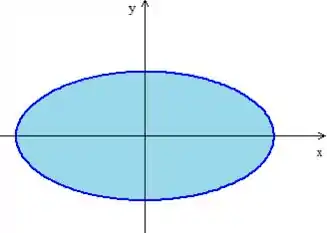
O enunciado diz que a região é a interior ao cilindro 4 x 2 + 16 y 2 = 1 . Então por hora, vamos apenas dizer que os parâmetros variam nessa região ai da elipse, ok? Depois se precisar, descrevemos em coordenadas polares.

Passo 3

Vamos achar agora o valor do nosso vetor normal

N → = ∂ φ ∂ x × ∂ φ ∂ y

φ x ,   y = x , y ,   x 2 + 2 y 2

Calculando cada derivada separadamente

∂ φ ∂ x = 1,0 ,   2 x

∂ φ ∂ y = 0 ,   1 ,   4 y

N → = i j k 1 0 2 x 0 1 4 y

= - 2 x , - 4 y , 1

Passo 4

O módulo da normal vai ficar

N → = - 2 x 2 + - 4 y 2 + 1 2

= 4 x 2 + 16 y 2 + 1

Passo 5

Juntando tudo na integral de área

∬ S N → d S = ∬ C 4 x 2 + 16 y 2 + 1   d x d y

Usando as coordenadas polares elípticas para calcular essa integral dupla...

x = 1 2 r cos ⁡ θ

y = 1 4 r sin ⁡ θ

J = 1 2 ⋅ 1 4 ⋅ r

Onde por x e y varia na elipse de mesmo a = 1 2 e b = 1 4 , o r varia de 0 até 1 e θ tem que dar uma volta completa, então...

0 ≤ r ≤ 1

0 ≤ θ ≤ 2 π

∬ C 4 x 2 + 16 y 2 + 1   d x d y = ∫ 0 2 π ∫ 0 1 4 1 4   r 2 cos 2 ⁡ θ + 16 1 16   r 2 sen 2 ⁡ θ + 1 ⋅ J   d r d θ =

∫ 0 2 π ∫ 0 1   r 2 cos 2 ⁡ θ + sen 2 ⁡ θ + 1 ⋅ r 8   d r d θ =

1 8 ∫ 0 2 π ∫ 0 1   r 2 + 1 ⋅ r   d r d θ

Fazendo uma mudança do tipo

r 2 + 1 = t       →               d t = 2 r d r         o u             r d r = d t 2

Trocando também os limites de integração...

r = 0             →                       t = 0 2 + 1 = 1

r = 1             →                       t = 1 2 + 1 = 2

1 16 ∫ 0 2 π ∫ 1 2   t d t d θ =

1 16 ∫ 0 2 π 2 3 t t 1 2 d θ = 1 16 2 3 2 2 - 2 3 ∫ 0 2 π d θ =

2 2 - 1 12 π  

Resposta

2 2 - 1 12 π

Exercícios de Livros Relacionados

Encontre a área da superfície com precisão de quatro casas decimais, expressando-a em termos de uma integral unidimensional e usando sua calculadora para estimar a integral.A Parte da superfície z = c
Calcule a integral de superfície. ∬ x 2 y z d S S é a parte do plano z = 1 + 2 x + 3 y que está acima do retângulo 0,3 × 0,2 .
Determine a área da superfície.A parte do cone z = x 2 + y 2 que se encontra entre o plano y = x e o cilindro y = x 2 .
Encontre a área da superfície com precisão de quatro casas decimais, expressando-a em termos de um a integral unidimensional e usando sua calculadora para estimar a integral.A Parte da superfície z =
Calcule a integral de superfície. ∬ x 2 + y 2 d S , S é a superfície com equação vetorial. r u , v =2 u v , u 2 - v 2, u 2 + v 2, u 2 + v 2 ≤ 1