Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Caso Escalar

Ver Teoria
Exercício 101234567891112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Áreas de superfícies

Determine a área da superfície z = x y que está dentro do cilindro x 2 + y 2 = 1 .

Passo 1

Vamos, antes de tudo, desenhar essa superfície para termos uma ideia melhor do problema. Temos um cilindro de raio 1 centrado na origem, que corta a superfície z = x y . Mas que superfície é essa? Você não precisa disso para resolver a questão, mas só para você poder visualizar, é uma cela “girada” no plano x y (ou seja, que não tem simetria nos eixos x e y , mas em eixos oblíquos a eles):

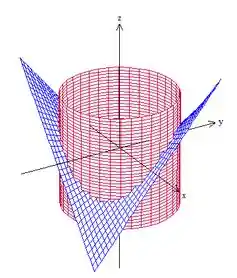
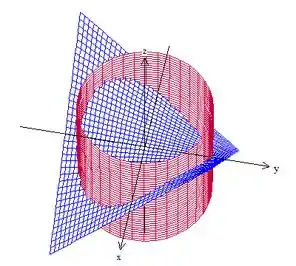
Como o problema pede a parte da superfície que estã dentro do cilindro, queremos isso aqui:

Vamos usar essa fórmula aqui para calcular a área da superfície:

A S = ∬ D   ∂ φ ∂ u × ∂ φ ∂ v d u d v

Passo 2

Agora precisamos parametrizar a superfície. Como nossa equação é z = x y , vamos usar x e y como parâmetros, ok? Temos então:

φ x ,   y = ( x , y , x y )

Onde

x 2 + y 2 ≤ 1

Essa é a projeção da nossa superfíce no plano x y , um círculo, pois a superfície azul é cortada pelo cilindro, lembra? Então, vista de cima, ela é um círculo.

Passo 3

Calcular ∂ φ ∂ x e ∂ φ ∂ y

∂ φ ∂ x = ( 1,0 , y )

∂ φ ∂ y = ( 0,1 , x )

Passo 4

Calcular N → x ,   y

N → x , y = ∂ φ ∂ x × ∂ φ ∂ y

N → x , y = 1,0 , y × 0,1 , x

N → x , y = i j k 1 0 y 0 1 x

N → x , y = ( - y ,   - x , 1 )

N → x , y = x 2 + y 2 + 1

Passo 5

Agora vamos montar a integral

A S = ∬ D   x 2 + y 2 + 1 d x d y

Onde D é o limite da superfíce azul, que já vimos que é dado por

x 2 + y 2 = 1

Passo 6

Agora isso aí virou questão de integral dupla, né? Precisamos escrever matematicamente essa região para levar os intervalos para integral.

Olha quantos quadrados nós temos. Nossa região de integração ainda é um círculo. Já sacou que temos que usar oordenadas polares, né? Temos então:

x = r cos ⁡ θ

y = r   s e n   θ

J = r

A região de integração passa a ser então 0 ≤ r ≤ 1 e 0 ≤ θ ≤ 2 π . Substituindo na integral, temos:

= ∫ 0 1 ∫ 0 2 π r r cos ⁡ θ 2 + r   s e n   θ 2 + 1   d θ d r =

= ∫ 0 1 ∫ 0 π 2 r r 2 + 1   d θ d r =

Passo 7

Agora vamos resolver a integral. Integrando em relação a θ :

= ∫ 0 1 θ r r 2 + 1 0 2 π   d r =

= 2 π ∫ 0 1 r r 2 + 1   d r =

Agora, para resolver essa integral, podemos fazer a substituição:

r 2 + 1 = u

2 r   d r = d u

Em resumo, chama tudo o que está dentro da raiz de u . Temos então

r = 1         →         u = 2

r = 0         →         u = 1

Levando isso para a integral, temos:

= π ∫ 1 2 u   d u =

Agora podemos integrar:

= 2 π 3   u 3 / 2 1 2 =

= 2 π 3 8 - 1 =

Resposta

2 π 3 2 2 - 1

Exercícios de Livros Relacionados

Encontre a área da superfície com precisão de quatro casas decimais, expressando-a em termos de uma integral unidimensional e usando sua calculadora para estimar a integral.A Parte da superfície z = c
Calcule a integral de superfície. ∬ x 2 y z d S S é a parte do plano z = 1 + 2 x + 3 y que está acima do retângulo 0,3 × 0,2 .
Determine a área da superfície.A parte do cone z = x 2 + y 2 que se encontra entre o plano y = x e o cilindro y = x 2 .
Encontre a área da superfície com precisão de quatro casas decimais, expressando-a em termos de um a integral unidimensional e usando sua calculadora para estimar a integral.A Parte da superfície z =
Calcule a integral de superfície. ∬ x 2 + y 2 d S , S é a superfície com equação vetorial. r u , v =2 u v , u 2 - v 2, u 2 + v 2, u 2 + v 2 ≤ 1