Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Caso Escalar

Ver Teoria
Exercício 471234567891011121314151617181920212223242526272829303132333435363738394041424344454648495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Considere a superfície parametrizada

r t ,   θ = t + 1 ,   t sen ⁡ θ ,   t cos ⁡ θ ,                   t ∈ 1 ,   2 ,   θ ∈ 0 ,   π ,

Cuja imagem denotaremos por S .

  1. Calcule uma equação implícita para S .
  2. Faça um esboço de S .
  3. É r uma superfície parametrizada regular ou não? Justifique a resposta.
  4. Calcule a equação implícita do plano tangente a S no ponto r 3 2 , π 2 .
  5. Calcule a integral de superfície

∬ S   6 x + π z d S

Passo 1

Letra a) Bem, se queremos uma equação implícita para essa parametrização, a primeira coisa que devemos fazer é pegar as posições x ,   y ,   z da parametrização.

Fazer isso é apenas atribuir x a primeira entrada de r , y a segunda e z a terceira, dessa forma aqui:

r t ,   θ = ( t + 1 ⏟ x ,   t sen ⁡ θ ⏟ y ,   t cos ⁡ θ ⏟ z )

Ou

x = t + 1

y = t sin ⁡ θ

z = t cos ⁡ θ

Pow, se a gente elevar esse y e esse z ao quadrado e somar, esse termo θ desaparece! Veja só

y 2 + z 2 = t sin ⁡ θ 2 + t cos ⁡ θ 2

Elevando esses termos ao quadrado e colocando em evidência o termo t 2 ...

y 2 + z 2 = t 2 sin 2 ⁡ θ + cos 2 ⁡ θ

Como já sabemos esse termo do parêntesis vale 1 lá da trigonometria, então...

y 2 + z 2 = t 2

Agora devemos desaparecer com esse termo t . Vamos fazer isso usando a única informação que não usamos ainda: x = t + 1 , logo t = x - 1 e portanto...

y 2 + z 2 = t 2     →           y 2 + z 2 = x - 1 2

Prontinho! Equação encontrada, item concluído!

Passo 2

Letra b) Então, para a gente começar aqui, você se lembra quem é o cara representado por essa equação implícita que encontramos? Essa equação representa um!... um cone;)

Mas cuidado! Não é qualquer cone. Esse cone aí tem o eixo em x e ele tem o seu vértice no x = 1 .

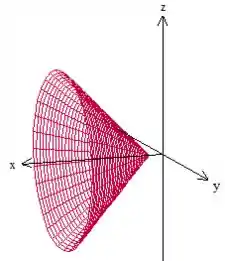
Mas calma, a gente não quer esse cone todo e é aqui que entra aquelas informações do problema: t ∈ 1 ,   2 ,   θ ∈ 0 ,   π .

Se t varia de 1 até 2 , x ,pela sua relação com t   x = t + 1 , varia de 2 até 3 . Percebeu? Então, nesse cone a gente não vai nem sequer chegar a pegar o vértice dele:

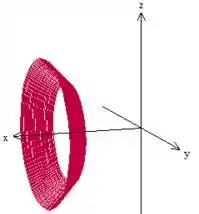
Vamos verificar a condição de θ ∈ 0 ,   π . Como essa superfície é classificada como uma superfície avançada de revolução, a gente já viu na teoria que o ângulo θ é aquele do fator de giro lembra? Como a gente gira em torno de x , esse ângulo aparece no plano Y Z .

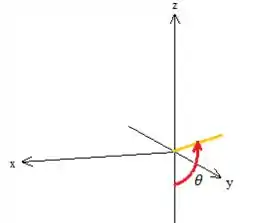
Como o nosso θ aqui varia de 0 até π , a nossa superfície S então será:

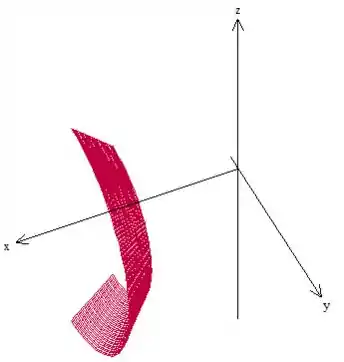
Passo 3

Pois bem, de acordo com a teoria, a parametrização dessa superfície apenas será regular se o vetor normal N → não zerar em todos os pontos. Então, bora calcular esse vetor normal N → .  

N → = ∂ r ∂ t × ∂ r ∂ θ

Calculando essas derivadas parciais da parametrização r t ,   θ = t + 1 ,   t sen ⁡ θ ,   t cos ⁡ θ :

∂ r ∂ t = 1 , sin ⁡ θ , cos ⁡ θ

∂ r ∂ θ = 0 , t cos ⁡ θ , - t sin ⁡ θ

Aplicando na fórmula do vetor normal:

N → = ∂ r ∂ t × ∂ r ∂ θ = i ^ j ^ k ^ 1 sin ⁡ θ cos ⁡ θ 0 t cos ⁡ θ - t sin ⁡ θ

Calculando o determinante...

i ^ j ^ k ^ 1 sin ⁡ θ cos ⁡ θ 0 t cos ⁡ θ - t sin ⁡ θ i ^ j ^   1 sin ⁡ θ   0 t cos ⁡ θ  

E calculando, vamos obter:

N → = - t sin 2 ⁡ θ   i ^ + t cos ⁡ θ   k ^ - - t sin ⁡ θ   j ^ + t cos 2 ⁡ θ   i ^

N → = - t sin 2 ⁡ θ   i ^ - t cos 2 ⁡ θ   i ^ + t sin ⁡ θ   j ^ + t cos ⁡ θ   k ^

Colocando em evidência o termo - t   i ^ :

N → = - t i ^ sin 2 ⁡ θ + cos 2 ⁡ θ + t sin ⁡ θ   j ^ + t cos ⁡ θ   k ^

N → = - t i ^ + t sin ⁡ θ   j ^ + t cos ⁡ θ   k ^

Mudando essa notação, concluímos que o vetor normal dessa superfície é:

N → = - t ,   t sin ⁡ θ , t cos ⁡ θ

Concluímos que a única forma desse vetor normal ser zero é se t = 0 , como isso não acontece no nosso caso pois t ∈ [ 1,2 ] , então a gente pode afirmar que a nossa superfície é regular para esta parametrização! ;)

Passo 4

Letra d) Man, se o problema já nos pediu que resolvesse o vetor normal dessa superfície, é porque ele quer que a gente utilize essa informação. Sim, mas como podemos fazer isso?

Se você se recordar um pouquinho lá da álgebra, se a gente tem o vetor normal do plano e um ponto do plano, a gente tem a equação desse plano.

Vamos começar aqui então vendo o que esse vetor normal tem a ver com isso:

Imagina que temos um vetor N → = ( A ,   B ,   C ) que é normal ao plano. Então a equação do plano é:

A x + B y + C z = D

Voltando para o nosso problema então, a gente pode determinar esse vetor N → utilizando a informação que queremos o plano tangente ao ponto 3 2 , π 2 :

N → = - t ,   t sin ⁡ θ , t cos ⁡ θ

N → = - 3 2 , 3 2 sin ⁡ π 2 , 3 2 cos ⁡ π 2

Simplificando...

N → = - 3 2 , 3 2 ,   0

Logo o nosso plano será:

- 3 2 x + 3 2 y + 0 z = D

Passo 5

Agora quem é esse D ? Vamos busca-lo utilizando o ponto que é comum ao plano e a superfície: Sim, ao ponto tangente! Substituindo 3 2 , π 2 na superfície r determinamos esse ponto:

r t ,   θ = t + 1 ,   t sen ⁡ θ ,   t cos ⁡ θ

r 3 2 , π 2 = 3 2 + 1 , 3 2 sen ⁡ π 2 , 3 2 cos ⁡ π 2

r 3 2 , π 2 = 5 2 , 3 2 ,   0

Esse ponto também é comum ao plano tangente, logo a gente substitui na equação do plano dessa forma aqui:

- 3 2 x + 3 2 y + 0 z = D

- 3 2 5 2 + 3 2 3 2 = D

D = - 6 4

Portanto o plano tangente é:

- 3 2 x + 3 2 y = - 6 4

Passo 6

Letra e) Bem, para começar a resolver essa integral basta aplicar a teoria de resolução de integrais de superfície no caso escalar:

∬ S   f x , y , z d S = ∬ R   f r t , θ . N → d t d θ

Então vamos lá, como a superfície já está parametrizada não precisamos ter esse trabalho, mas necessitamos encontrar a norma do vetor normal N → = - t ,   t sin ⁡ θ , t cos ⁡ θ :

N → = - t 2 + t sin ⁡ θ 2 + t cos ⁡ θ 2

Calculando os quadrados...

N → = t 2 + t 2 sin 2 ⁡ θ + t 2 cos 2 ⁡ θ

Colocando t 2 em evidência e lembrando que sin 2 ⁡ θ + cos 2 ⁡ θ = 1 ...

N → = t 2 1 + sin 2 ⁡ θ + cos 2 ⁡ θ

N → = t 2 1 + 1 = t 2

Substituindo agora as variáveis da parametrização r em f x ,   y ,   z = 6 x + π z , ou seja,

r t ,   θ = t + 1 ,   t sen ⁡ θ ,   t cos ⁡ θ

Trocando tudo...

f x ,   y ,   z = 6 x + π z

f r ( t ,   θ ) = 6 t + 1 + π t cos ⁡ θ

Jogando todos esses ingredientes na integral, teremos:

∬ R   f r t , θ . N → d t d θ = ∬ R   6 t + 1 + π t cos ⁡ θ ∙ t 2   d t d θ

Como R é o intervalo dos parâmetros, teremos

∫ 0 π ∫ 1 2 6 2 t 2 + t + π t 2 cos ⁡ θ d t d θ

Passo 7

Resolvendo a integral dupla calculando primeiro a integral de dentro, ou seja, em relação a t

6 2 ∫ 0 π ∫ 1 2 t 2 + t + π t 2 cos ⁡ θ d t d θ =

6 2 ∫ 0 π t 3 3 + t 2 2 + π t 3 3 cos ⁡ θ 1 2 d θ =

Substituindo os limites de integração

6 2 ∫ 0 π 2 3 3 + 2 2 2 + π 2 3 3 cos ⁡ θ - 1 3 3 - 1 2 2 - π 1 3 3 cos ⁡ θ d θ =

6 2 ∫ 0 π 7 3 + 3 2 + 7 π 3 cos ⁡ θ d θ =

Agora calculando essa integral em relação a θ

6 2 7 3 θ + 3 2 θ + 7 3 π ( sin ⁡ θ ) 0 π =

Substituindo os limites de θ

∬ S   6 x + π z d S = 6 2 7 3 π + 3 2 π = 23 2 π

Resposta

  1. y 2 + z 2 = x - 1 2

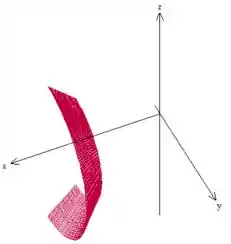
  3. r é uma superfície parametrizada regular.
  4. - 3 2 x + 3 2 y = - 6 4

∬ S   6 x + π z d S = 23 2 π

Exercícios de Livros Relacionados

Encontre a área da superfície com precisão de quatro casas decimais, expressando-a em termos de uma integral unidimensional e usando sua calculadora para estimar a integral.A Parte da superfície z = c
Calcule a integral de superfície. ∬ x 2 y z d S S é a parte do plano z = 1 + 2 x + 3 y que está acima do retângulo 0,3 × 0,2 .
Determine a área da superfície.A parte do cone z = x 2 + y 2 que se encontra entre o plano y = x e o cilindro y = x 2 .
Encontre a área da superfície com precisão de quatro casas decimais, expressando-a em termos de um a integral unidimensional e usando sua calculadora para estimar a integral.A Parte da superfície z =
Calcule a integral de superfície. ∬ x 2 + y 2 d S , S é a superfície com equação vetorial. r u , v =2 u v , u 2 - v 2, u 2 + v 2, u 2 + v 2 ≤ 1