onde é a parte da esfera interior ao cone ;
Passo 1
E aí gente bonita, como vocês estão?
Nessa questão temos que calcular a nossa famosa integral de superfície no caso escalar (não temos um campo vetorial).
Vocês lembram a receita do bolo pra calcular esse tipo de integral?

Hahaha! Então bora dar uma revisada nos passos!
Imagina que temos que calcular:
Parametrizar a superfície
Escrever a função como função da parametrização
Calcular o módulo do vetor normal à superfície, usando que:
Montar a integral:
Resolver como uma integral dupla normal!
Show de bola gente! Essa é a receitinha de bolo pra gente matar qualquer integral de superfície no caso escalar.
Então, bora usar essa ideia na integral pedida no enunciado e matar mais um item 😊
Passo 2
No caso desse item precisamos resolver a integral:
Assim, vemos que a função que está sendo integrada é:
onde é a parte da esfera interior ao cone .
Pra entender melhor quem é a superfície vamos esboçá-la:
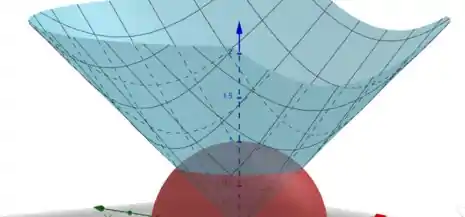
A superfície é justamente a superfície da esfera que está “dentro” do cone.
Vamos seguir a nossa receita de bolo pra matar essa integral de superfície.
Parametrizar a superfície :
Para fazer isso usaremos a parametrização em coordenadas esféricas, já que é uma calota esférica (intersecção de um cone com uma esfera).
Como:
Temos que essa esfera tem raio .
O grande ponto é conseguirmos saber como estão variando e .
Como a superfície trata-se de uma calota, podemos afirmar que:
Pois uma calota é formada por várias seções circulares completas.
Já em , precisamos determinar o valor mínimo do seu cosseno, para a partir daí descobrir o valor máximo de .
Temos:
Substituindo a primeira equação na segunda, teremos:
Logo, o cosseno de , vale:
Assim:
Portanto, temos também que:
Perfeito!
A nossa parametrização ficou:
Muito bom!!
Passo 3
Seguindo nossa receitinha, temos agora:
Escrever a função como função da parametrização:
Lembra que vimos:
Mas, pela parametrização:
Logo:
Calcular o módulo do vetor normal à superfície, usando que:
Vamos lá, encontramos que:
Assim:
Já se tomarmos a derivada parcial com relação a , teremos:
Muito bom! Vamos então calcular o produto vetorial:
Esse é justamente o vetor normal! Precisamos apenas calcular o seu módulo!
Perfeito!
Montar a integral:
Usando os dados que encontramos, temos:
Então, nossa missão é resolver essa integral!
Passo 4
Vamos resolver a integral:
Como é constante em relação a integral mais interna:
Vamos começar pela segunda integral:
Lembrando que:
Temos:
Logo:
Mas, se essa integral é nula, independente do resultado da outra integral, teremos que:
Prontinho! Matamos mais uma questão 😊
Obrigado pela atenção galera!