Calcule a área da superfície do cone situada entre os planos e .
Passo 1
Começamos com a parametrização da superfície em questão. Como se trata de um cone, é razoável utilizar coordenadas esféricas ou cilíndricas. Entretanto, uma coisa que devemos sempre prestar atenção é nas equações das superfícies que limitam a que queremos descobrir a área.
Como se tratam de planos, não é adequada nenhuma parametrização que envolva funções trigonométricas (i.e. cilíndrica e esférica). Portanto, a melhor parametrização que conseguimos obter é a explícita...
Encontrando em função de e obtemos:
Podemos perceber que são duas parametrizações possíveis. Afinal de contas o cone tem uma parte superior e uma inferior. Como estamos integrando entre e um outro plano, podemos observar pelos cortes desses planos que só precisamos parametrizar a parte superior do cone.
Se você não tiver a intuição de qual corte fazer, tente todos os três possíveis: , , . Basta em cada um igualar uma das variáveis à uma constante (geralmente zero).
No plano , que é o plano , temos essa revelação. Neste plano o corte do cone é:
Representado em laranja. Ao passo que o corte do plano:
É representado em azul.
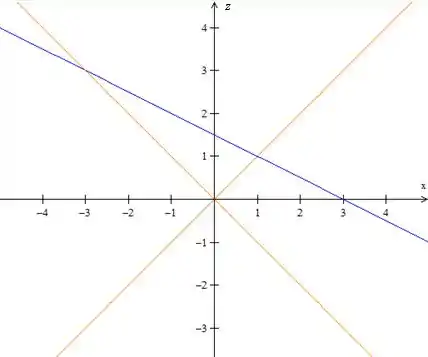
Portanto:
Passo 2
Vamos determinar agora as limitações da superfície em termos da nossa parametrização:
Agora vamos ver como é que o outro plano encontra com o nosso cone:
Substituindo na equação do cone:
Completando o quadrado perfeito:
Como chegamos à esse negócio mesmo? Ah sim, nós igualamos a equação do plano à do cone. Então nós conseguimos encontrar a equação dos pontos que pertencem tanto à um quanto ao outro. Por consequência, a região dos pontos do cone que estão entre um plano e outro é dos pontos que estão no interior desta elipse:
Ou seja, nossa parametrização é:
Ao passo que nosso domínio é:
Dá pra ver que não vai dar muito certo fazer essa conta aí por causa do domínio... Mais tarde voltaremos nisso.
Passo 3
Para aplicar a fórmula da área precisamos do módulo do vetor normal:
Calculando as derivadas parciais:
Fazendo o produto vetorial:
E calculamos o módulo:
Passo 4
Aplicando a fórmula, temos:
Sendo que:
O detalhe é que fazer essa conta obviamente não vai ser agradável... Vamos trocar de coordenadas por favor? Implementando coordenadas polares, obtemos:
Daí tiramos que nosso domínio vai ser:
Falta só calcular o Jacobiano para trocar de variáveis. Lembrando lá das mudanças polares
Substituindo na integral os limites de integração junto com o jacobiano:
Como são independentes nos limites de integração as variáveis e , separamos as integrais:
Finalmente encerramos!