4) Calcule a área das superfícies:
h) parte do cone , que se encontra dentro do cilindro , fora do cilindro .
Passo 1
Para fazer o cálculo dessa área, vamos precisar usar a integral de superfície descrita por
Vamos ter que fazer bastante coisa pra chegar nessa integral certinha: primeiro vamos achar uma parametrização para a superfície, achar os seus limites e por fim o módulo do vetor normal, quando fizermos isso, vamos voltar pra integral e resolver!
Começando pela parametrização da superfície, o esboço dela é esse aqui:
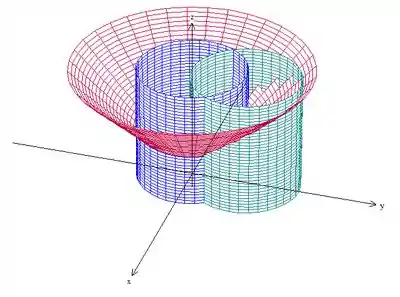
O exercício pede a superfície do cone, né? Então vamos usar os cilindros somente para limitar as variáveis, a parametrização mesmo vai ser a do cone. Uma possível é a seguinte:
Passo 2
Projetando as superfícies dos cilindros no plano fica assim
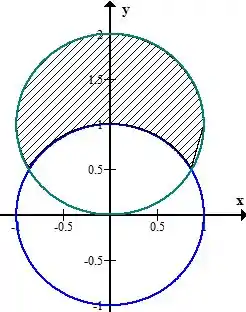
O enunciado diz primeiro que a região é a interior ao cilindro , substituindo os parâmetros:
Obs: Se você ficar na dúvida se o símbolo deve ser ou uma dica é escolher um ponto que você sabe que está dentro da sua região! Para esse ponto a inequação deve ser verdadeira, por exemplo, está dentro da região, substituindo ali em cima:
Que é verdadeiro! Se tivéssemos colocado um sinal de maior () daria errado. Voltando para a questão:
O segundo limite é exterior ao cilindro , com isso
Não pegamos o valor negativo pois é sempre positivo. Os seus limites, portanto, são:
Os limites de podemos descobrir por essa relação de encontrada acima. Perceba que, se é maior que e é maior que , podemos concluir que
Passo 3
Vamos achar agora o valor do nosso vetor normal
Calculando cada derivada separadamente
Passo 4
O módulo da normal vai ficar
Passo 5
Juntando tudo na integral de área
Aqui vamos lembrar da seguinte relação:
Voltando pra integral
Aqui vamos lembrar que o seno dos ângulos replementares (que têm soma igual a ) são opostos, ou seja