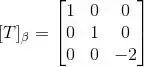Seja uma transformação linear dada por:
(a) Obtenha o polinômio característico e calcule os autovalores de T.
(b) Obtenha para cada um dos autovalores de T uma base para seu respectivo autoespaço (subespaço associado).
(c) T é diagonalizável? Justifique. Em caso afirmativo, determine uma base na qual a matriz de T é uma matriz diagonal e exiba tal matriz.
Passo 1
(a) Vamos começar achando a matriz que representa a transformação linear T na base canônica.
Para isso, basta fazer uma “decomposição” da transformação linear dada, colocando na primeira coluna os coeficientes do x em cada coordenada, na segunda coluna os coeficientes do y em cada coordenada e por último na terceira coluna os coeficientes do z em cada coordenada.
Ficamos com a matriz:
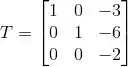
Agora pra achar os autovalores da transformação T, achamos os autovalores dessa matriz aí.
Fazendo isso:
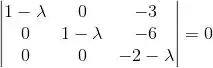
Esse é o polinômio característico de T.
Os autovalores são:
Passo 2
(b) Vamos usar a definição de autovalor e autovetor para achar os autovetores.
Para , temos:
Pela terceira equação:
Então os autovetores associados a esse autovalor são do tipo:
Esses dois vetores são LI e todo autovetor é uma combinação linear deles.
Logo, uma base para o autoespaço associado a é:
Fazendo a mesma coisa para
Da primeira equação:
Da segunda equação:
Logo, os autovetores associados a esse autovalor são do tipo:
Portanto uma base para o autoespaço associado a é:
Passo 3
(c) Note que:
É uma base de formada por autovetores de T.
Como existe essa base, T é diagonalizável.
Sua representação diagonal é uma matriz diagonal que possui os autovalores na diagonal principal, respeitando a ordem dos autovetores da base :
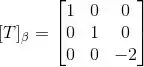
Resposta
(a) Polinômio característico:
Autovalores: e
(b)
(c)