Ache os pontos sobre a curva para os quais a reta tangente é horizontal

E ai galera, tudo bem?

Essa questão parece complicada, mas vou ajudar você aqui! Bora lá?

O problema deu a equação de uma curva

E pediu para achar todos os pontos para os quais a reta tangente é horizontal

Mas calma lá! O que tem a ver a reta tangente com uma curva?

y em um determinado ponto

A equação de uma reta qualquer é

Onde é o coeficiente angular e o linear.

E aqui que quero fazer a ligação com uma curva! Quando falamos em reta TANGENTE a uma função/curva, dizemos que essa reta toca nessa curva em um ÚNICO ponto! Como por exemplo nessa curva qualquer em azul aqui embaixo e no ponto P temos uma reta tangente em vermelho

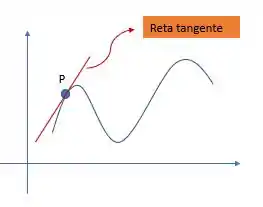E a inclinação da reta tangente nesse ponto é justamente a derivada da curva nesse ponto!

Sendo assim, podemos associar aquele da reta com a derivada de em um ponto

Beleza?

Mas o problema nos pede os pontos em que a reta tangente é HORIZONTAL

Uma reta horizontal tem inclinação?

A resposta é não!

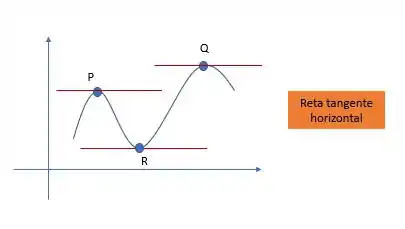
Quando uma reta é horizontal, dizemos que ela não tem inclinação, ela não está nem subindo, nem descendo, a inclinação é zero! Igualzinho a inclinação dessas retas do desenho ali em cima, podemos ter várias em uma curva. Sempre onde a curva/função tiver um máximo (exemplo dos pontos P e Q) ou um mínimo (ponto R) a derivada vai ser zero, ou seja, a inclinação da reta tangente é zero!

E é isso que o problema pede! Determinar os pontos da curva tem uma reta tangente horizontal significa descobrir onde a derivada dessa curva é zero!

Então o que precisamos fazer é derivar e igualar a zero, e assim determinar todos os pontos onde isso acontece