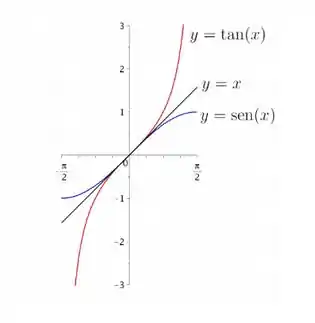
Considere as funções e , ambas definidas no intervalo .
a) Os gráficos das funções f e g possuem ponto de tangência? Se sim, determine as coordenadas do(s) ponto(s) de tangência e a(s) equação(ões) da(s) reta(s) tangente(s) compartilhada(s) pelos dois gráficos nesse(s) ponto(s).
b) Esboce abaixo os gráficos funções f e g (indique ao lado de cada curva a sua respectiva
equação). Caso tenha(m) sido encontrado(s) ponto(s) de tangência no item anterior, esboce
também a(s) reta(s) tangente(s) aos gráficos das funções f e g no(s) ponto(s) de tangencia.
Passo 1
a) Para que as funções e se tangenciem em um ponto que vamos chamar de , duas coisas precisam acontecer simultaneamente:
E
Podemos montar um sistema com essas duas condições para tentar descobrir o ponto que está condido no intervalo .
Da pra tirar alguma conclusão desse sistema? Sim ne? A equação
só é verdadeira se . Felizmente esse valor de também satisfaz a primeira equação:
Isso significa, então, que e se tangenciam no ponto .
Passo 2
Falta achar a reta tangente compartilhada pelos dois gráficos nesse ponto (é só uma porque só há um ponto de tangencia). A equação da reta tangente a uma função em um ponto qualquer é dada por:
Como queremos uma reta compartilhada pelas duas funções, as equações das retas tangentes de cada uma das funções no ponto (0,0) tem que ser iguais, ou seja:
Sabemos que:
Portanto:
Passo 3
b) Incluindo o ponto de tangencia e a reta tangente , calculados no item (a), o gráfico fica assim:
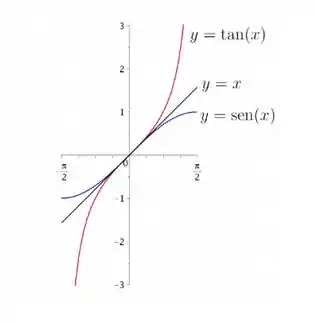
Resposta
a) e
b)