Considere a função definida pelo gráfico abaixo,
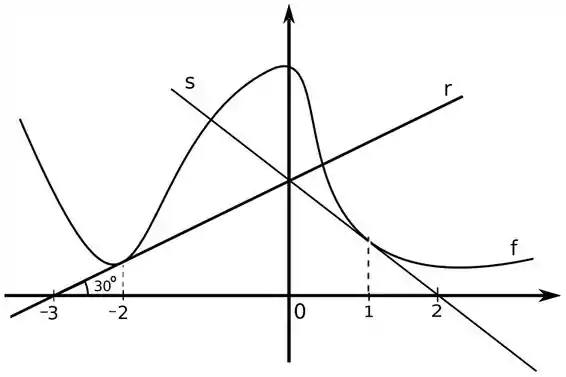
Sabendo que a reta é tangente ao gráfico da em e a reta tangente ao gráfico da em
- Determine a equação da reta
- Determine e
- Determine a equação da reta
- Determine e
Passo 1
Vamos começar pela letra .
Olhando para a equação da reta tangente:
Temos que é o ponto de tangência. Mas se olharmos pro enunciado vamos ver que a reta é tangente em , então:
Substituindo:
Olhando o gráfico, é perceptível que a reta que queremos calcular toca o eixo no ponto .
Então é um ponto dessa reta. Assim:
Portanto:
Passo 2
Tá, mas qual o valor de ? Aí vem a outra sacada. No gráfico também está o ângulo de inclinação da reta. A tangente desse ângulo é seu coeficiente angular que também será a derivada da curva naquele ponto:
Já temos todos os valores agora:
Se a gente ajeitar melhor, vamos chegar que equação da reta é:
Passo 3
Vamos para a letra agora.
Já na letra vimos que:
Opa! Já matamos😊
Passo 4
Letra (tá acabando)!
Considerando a equação geral da reta tangente de novo, mas agora para :
Pelo gráfico do enunciado o ponto de tangencia da reta é em :
Assim, a equação ficará:
Ainda temos mais algumas coisas aí. Assim, como aconteceu com , a reta também cruza o eixo , mas quando . Logo passa pelo ponto usando isso temos:
Show! Mais uma relação maneira, então dá para escrever:
Passo 5
Como achar ? Olhando para o gráfico (sempre ele), vemos que as retas e se encontram quando . Assim, nesse ponto temos que:
Mas encontramos
E
Substituindo e igualando :
Finalmente, substituindo esse valor em e aí temos que a equação da reta é:
Passo 6
Acabou? Quase, porque a letra a gente tira fácil desta relação que encontramos na :
Sendo:
Que também foi calculado anteriormente, então: