Considere a função definida pelo gráfico abaixo, a reta tangente ao gráfico da em e a reta tangente ao gráfico de em .
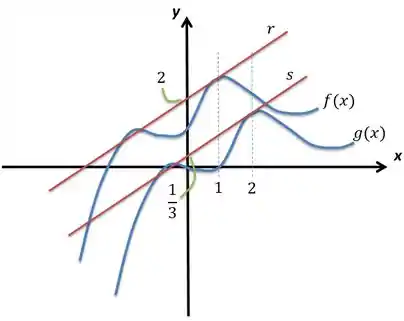
Determine:
A equação das retas e
Passo 1
O objetivo é descobrir a equação das duas retas que passam tangentes a em e a em . Antes de desenvolver mais, repara que elas (retas e ) parecem ter a mesma inclinação. De fato elas têm! Sabe por que? Repara:
Se usarmos :
No fim das contas notamos que o é simplesmente deslocado uma unidade para baixo. Concluímos que a curvatura da função no ponto será a mesma. Isso significa que a derivada é igual a o que faz com que as retas tangentes aos gráficos nesses pontos tenham os mesmos coeficientes angulares. Enfim, elas têm a mesma inclinação, a reta e .
Passo 2
Agora vamos pensar propriamente nas retas. A reta toca o eixo no e a reta toca o eixo em . Esses são seus respectivos coeficientes angulares. Vou chamar seus coeficientes angulares, como ainda não o conheço, de :
Mas a gente sabe que passa no ponto e no ponto . Vamos substituir isso nas equações:
O detalhe é que sabemos que
Agora é só resolver!
Passo 3
Logo, temos
Passo 4
Para descobrir temos que lembrar que o coeficiente angular da reta tangente ao gráfico num ponto vale a sua derivada. Ou seja,
Passo 5
Para descobrir basta voltar ao sistema que usamos para resolver as retas: