UERJ, Sem Campus, Cálculo I, Listas de C1 - Profº Rubens Sucupira - Lista 3, Questão 5
Encontre uma equação para a reta tangente à curva que seja paralela à reta tangente à curva no ponto (1, 2).
Passo 1
Eaew, belezinha?
A questão pede para a gente encontrar uma reta tangente que seja paralela à uma segunda reta. Bem, a gente sabe que retas são funções bastante simples, porque só precisamos de dois parâmetros para determinar suas equações: Seu coeficiente angular a e seu coeficiente linear b, pois qualquer reta pode ser escrita na forma:
Então, primeiro precisamos determinar qual é a equação da reta tangente à curva no ponto (1,2) para obter sua inclinação e, em seguida, determinar a equação da reta tangente à curva . E como a gente determina a inclinação de uma reta tangente à uma função? Calculando a sua derivada no ponto. Então vamos lá derivar!
Passo 2
Como a derivada de uma função do tipo é simplesmente
E, como podemos escrever a função como , temos que a sua derivada é:
Então, a inclinação da reta tangente no ponto de coordenadas (x = 1, y = 2) é simplesmente:
Ótimo! Agora a gente já sabe a inclinação que a reta tangente à função precisa ter para ser paralela a reta da função : 1! Então, agora só precisamos derivar a função para determinar quando a inclinação de sua reta tangente é igual à 1. Então bora lá!
Passo 3
Novamente, a nossa função é uma função polinomial do tipo . Então, a sua derivada é dada por
A gente quer que essa inclinação seja igual à 1. Então só precisamos igualar a expressão acima à 1 e obter o valor de x para o qual isso ocorre:
Então, no ponto de coordenadas , a inclinação da reta tangente é igual à 1 e, portanto, ela é paralela à reta tangente à função no ponto (1,2). Agora, para terminar de determinar a reta, só precisamos calcular seu coeficiente linear. E como a gente faz isso? Bem, se a reta que a gente quer determinar é tangente à função no ponto , isso significa que esse ponto pertence tanto à função quanto à reta.
Sabendo a inclinação a e um ponto da reta, podemos determinar a equação que descreve a reta inteira fazendo:
Então, a equação da reta tangente à curva x²-4 paralela a curva no ponto (1,2) é
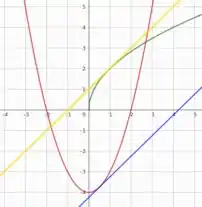
Dá só uma olhada no gráfico das funções , , e , respectivamente em, verde, vermelho, azul e amarelo:
