ME03) Seja uma função qualquer, e considere as afirmações abaixo:
- A reta tangente a em um dado ponto pode interceptar seu gráfico em outro ponto
- possui reta tangente em todo ponto de seu gráfico
Escolha a alternativa correta:
- Ambas são falsas
- Ambas são verdadeiras
- é falsa e é verdadeira
- é verdadeira e é falsa
Passo 1
Vamo que vamo. A letra está falando que a equação da reta tangente em um ponto pode tocar a função outra vez. Bem, se pensarmos na reta tangente de algumas funções, vai parecer que a é falsa:
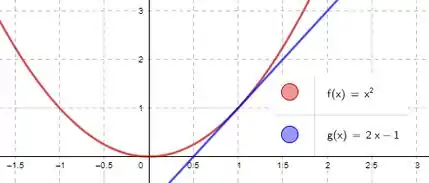
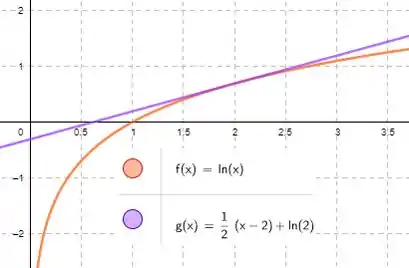
Mas sabe o que essas funções tem em comum que limitam a criatividade? Ou elas são estritamente crescentes/decrescentes ou possuem máximo/mínimo global. E se tivéssemos máximos e mínimos locais? Saca só alguns exemplos:
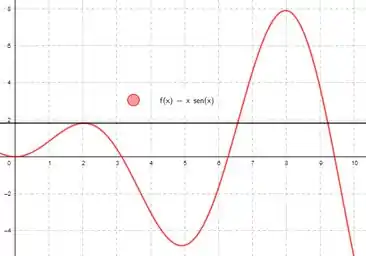
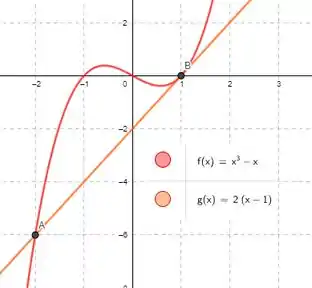
Viu só? Pensar em funções diferentes abriu nossos olhos. Logo a letra é verdadeira em!
Passo 2
Vamos lá, agora a letra está dizendo que não importa quem seja , ela sempre terá uma reta tangente a um ponto. Oras, pra isso ser verdade, a função tem que ser derivável em todos os pontos e, logo, contínua. Se tivermos por exemplo:
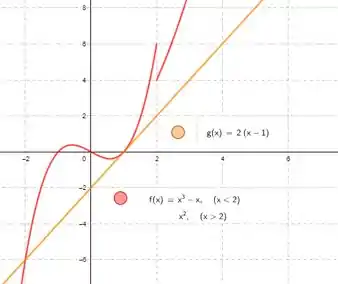
Esse exemplo em cima na verdade é muito bom porque mostra uma função que pode ter reta tangente tocando a função em outro ponto diferente do ponto de tangência e mostra que a função pode não ter derivada em algum ponto, como é o caso do ponto .
Resposta correta vai ser então é a letra